描述
內容簡介
|
☆★☆★【有如手術刀般精準!利用Python幫你管控財金風險!】★☆★☆
在上一本基礎篇的學習完備,能善用Python程式語言及常用的工具套件之後,接下來就是開始對金融風險進行評估了。
本書接續介紹了各種數學模型,包括波動性、隨機過程及相當重要的馬可夫過程、馬丁格爾、隨機漫步、維納過程等,另外也包含蒙地卡羅等數學模型的應用。
而統計科學中最常用的回歸,本書也有涉獵。另外包括了二元樹、BSM選擇權、希臘字母,市場風險等,都有最完整的Python程式和數學公式供讀者計算、運用。
金融商品龐大且複雜,需要像使用手術刀般精準、細緻地切割每一個細節,畢竟賠錢事小,沒辦法掌握到大盤的迅速波動與走勢,才是一大損失。
本書看點 ✪了解金融商品的波動性、移動平均、ARCH、GARCH。 ✪認識蒙地卡羅股價模擬、歐式、亞洲式選擇權。 ✪學習市場風險分類、度量、價值、分析。 ✪精進交易對手信用風險、投資組合理論、無差別效用曲線、資產定價理論。 |
作者
| 姜偉生
博士,FRM,現就職於MSCI,負責為美國對沖基金客戶提供金融分析產品RiskMetrics RiskManager的諮詢和技術支援服務。MATLAB建模實踐超過10年。跨領域著作豐富,在語言教育、新能源汽車等領域出版中英文圖書超過15種。
塗升 博士,FRM,現就職於CMHC(Canada Mortgage and Housing Corporation,加拿大抵押貸款和住房管理公司,加拿大第一大皇家企業),從事金融模型審查與風險管理工作。曾就職於加拿大豐業銀行,從事IFRS9信用風險模型建模,執行監管要求的壓力測試等工作。MATLAB使用時間超過10年。 |
目錄
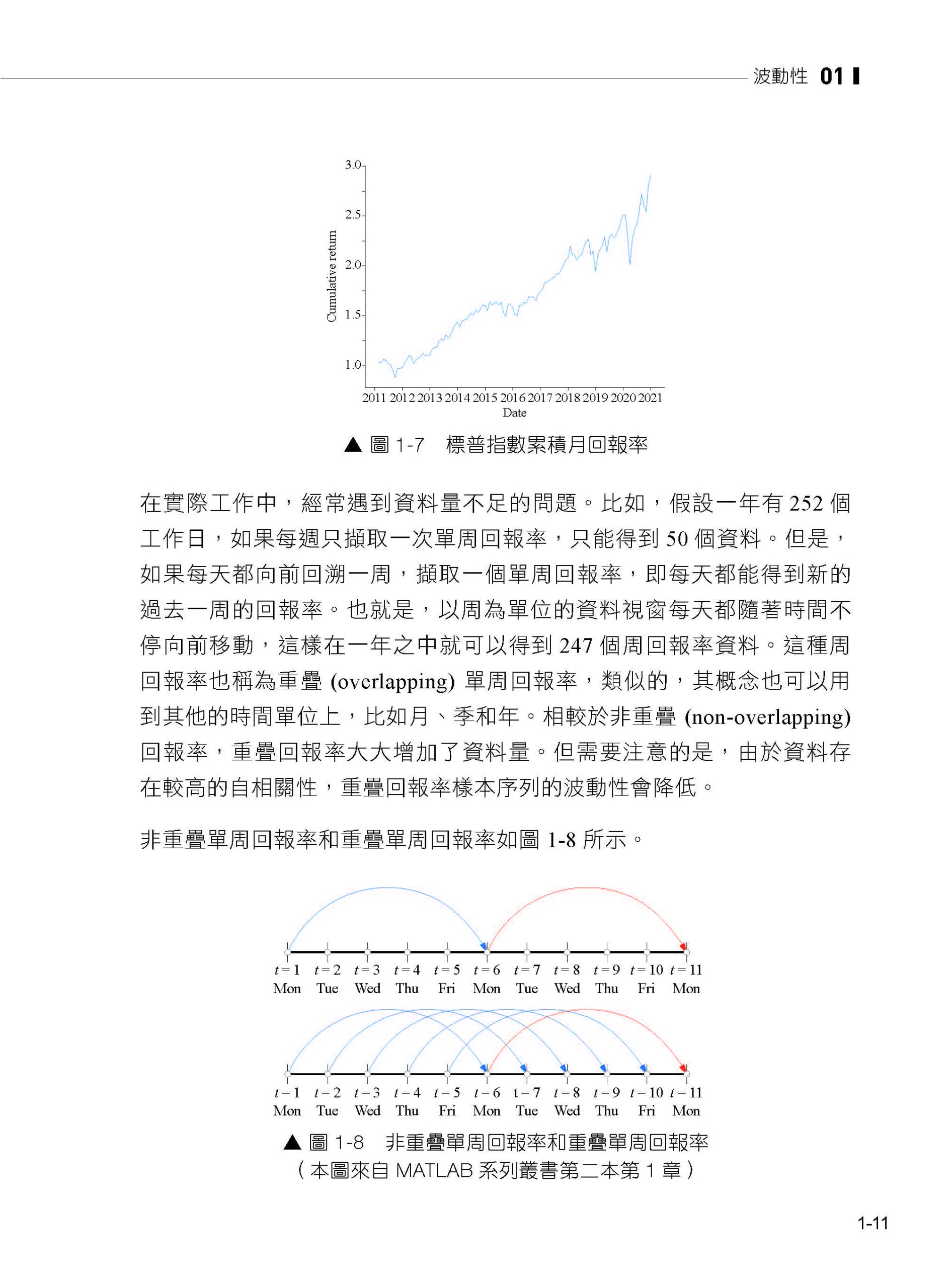
| 第1章 波動性
1.1 回報率 1.2 歷史波動性 1.3 移動平均(MA)計算波動性 1.4 自回歸條件異方差模型ARCH 1.5 廣義自回歸條件異方差模型GARCH 1.6 波動性估計 1.7 隱含波動性
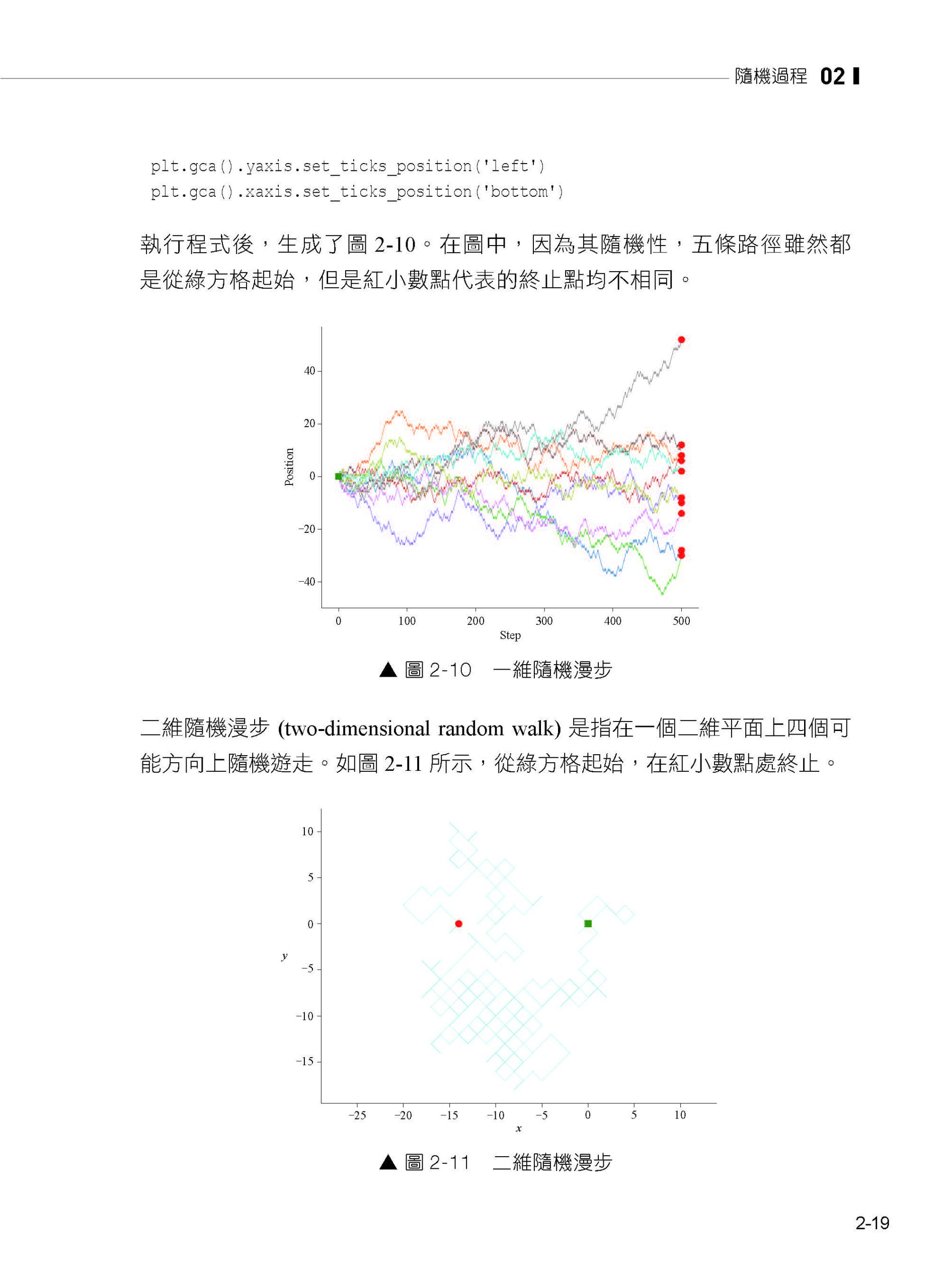
第2章 隨機過程 2.1 隨機變數與隨機過程 2.2 馬可夫過程 2.3 馬丁格爾 2.4 隨機漫步 2.5 維納過程 2.6 伊藤引理 2.7 幾何布朗運動
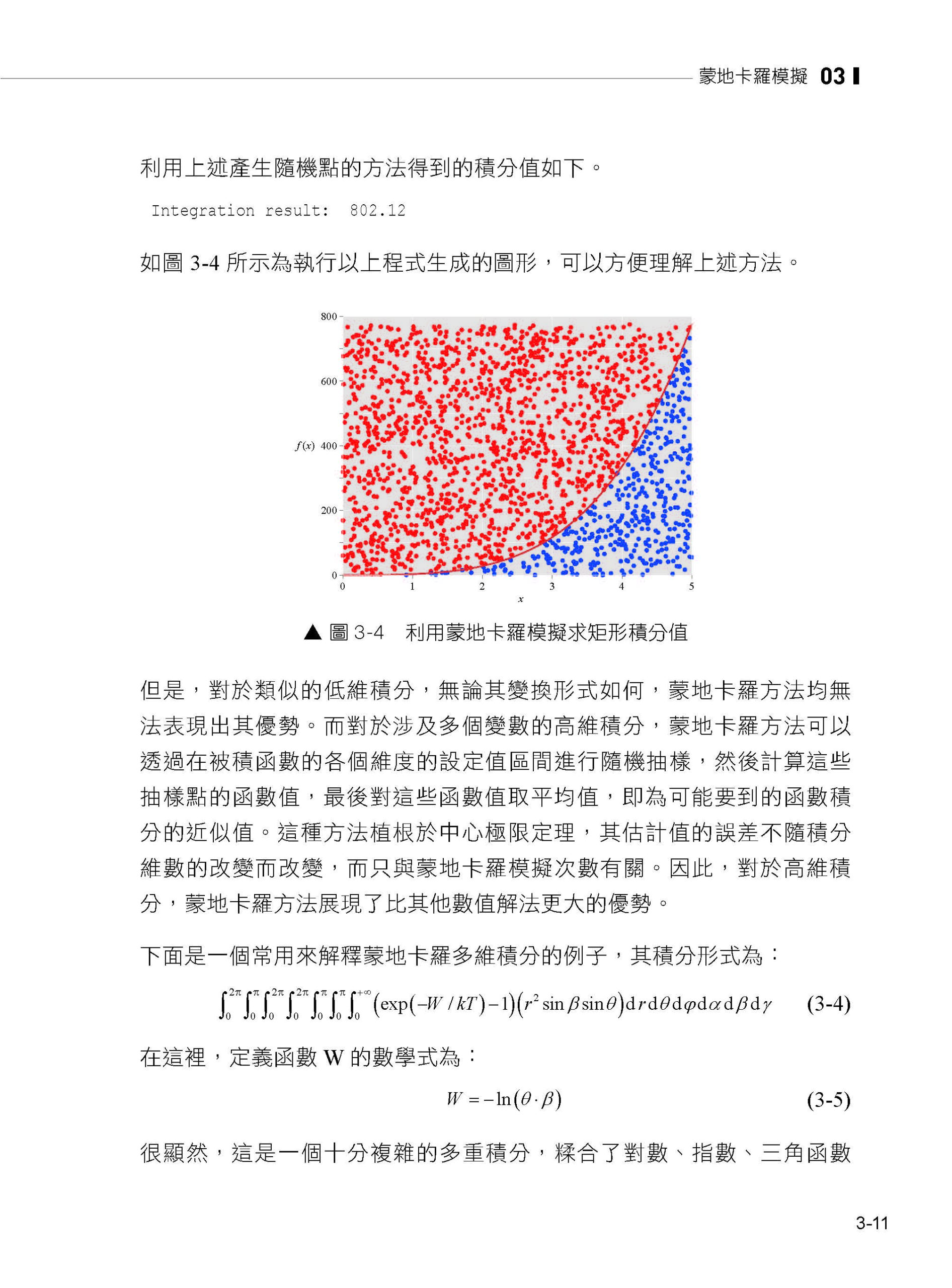
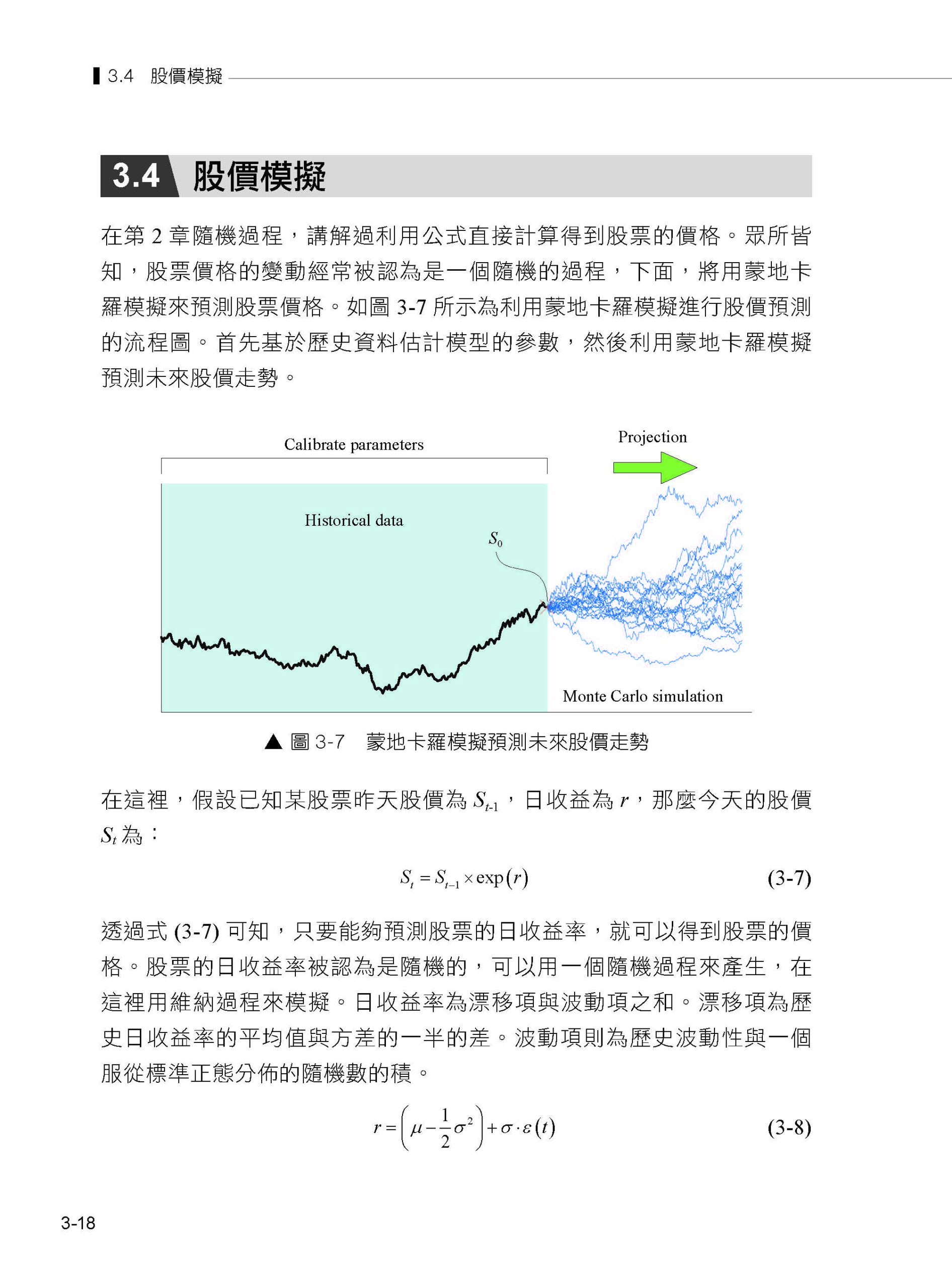
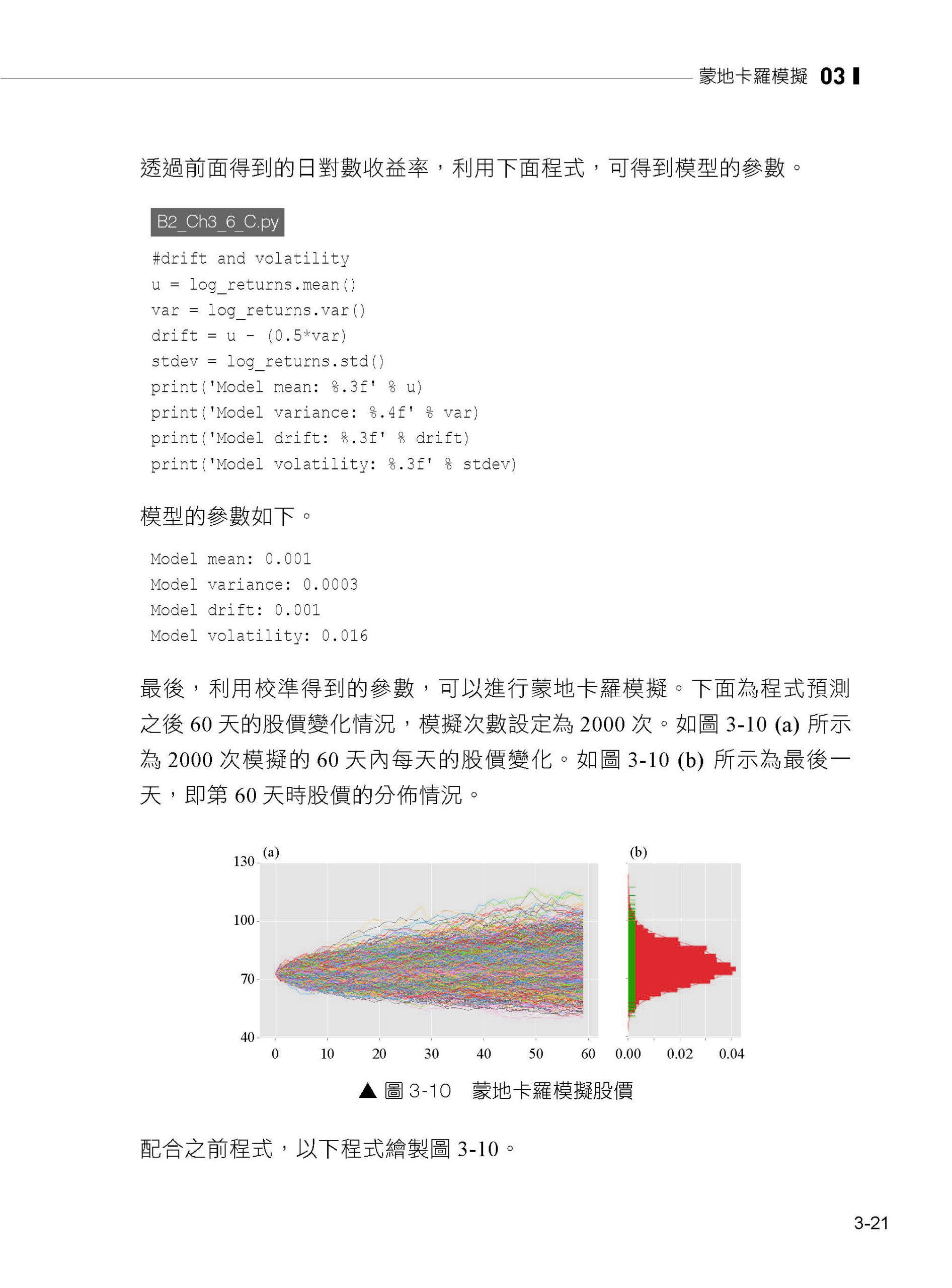
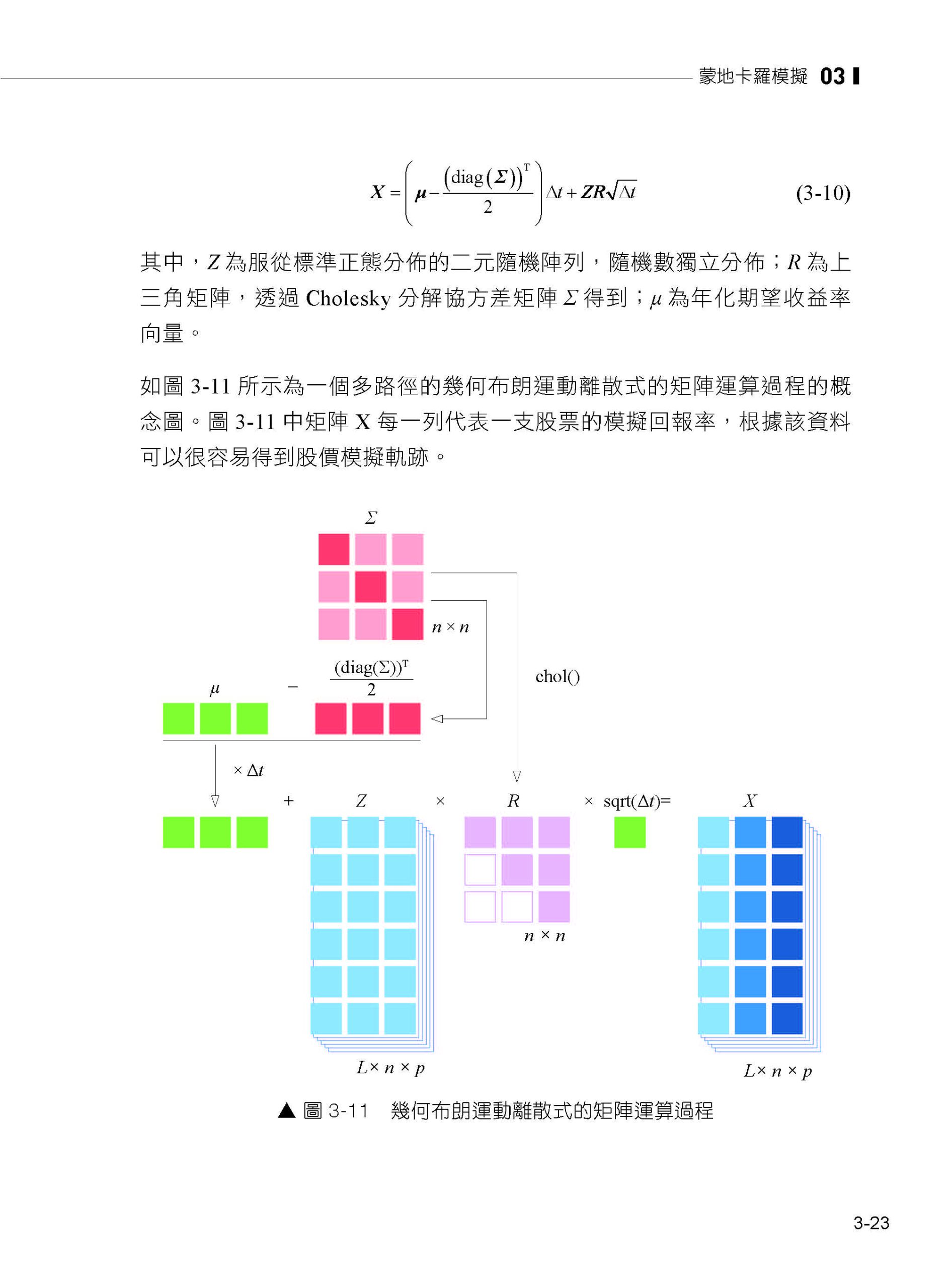
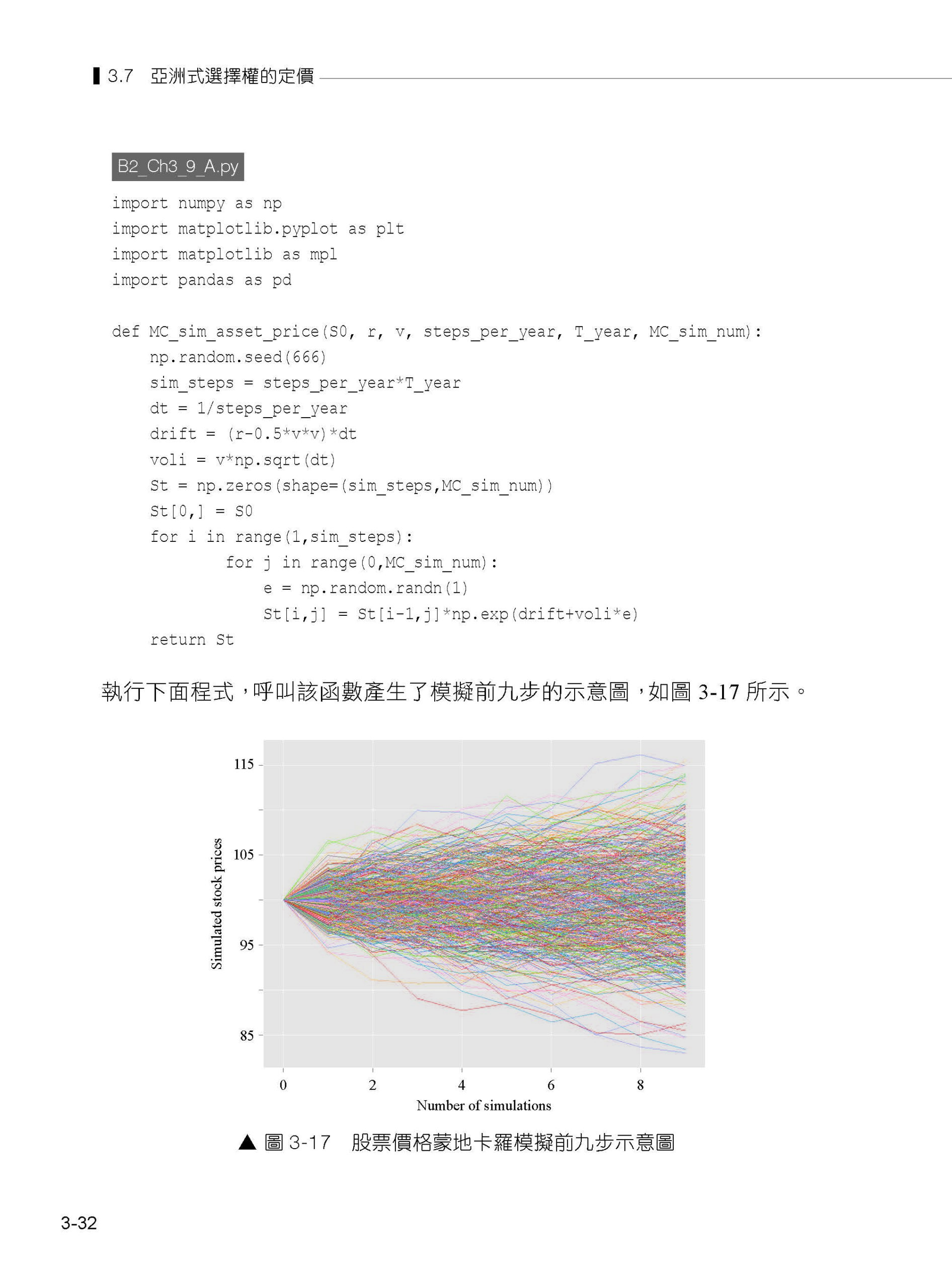
第3章 蒙地卡羅模擬 3.1 蒙地卡羅模擬的基本思想 3.2 定積分 3.3 估算圓周率 3.4 股價模擬 3.5 具有相關性的股價模擬 3.6 歐式選擇權的定價 3.7 亞式選擇權的定價 3.8 馬可夫鏈蒙地卡羅
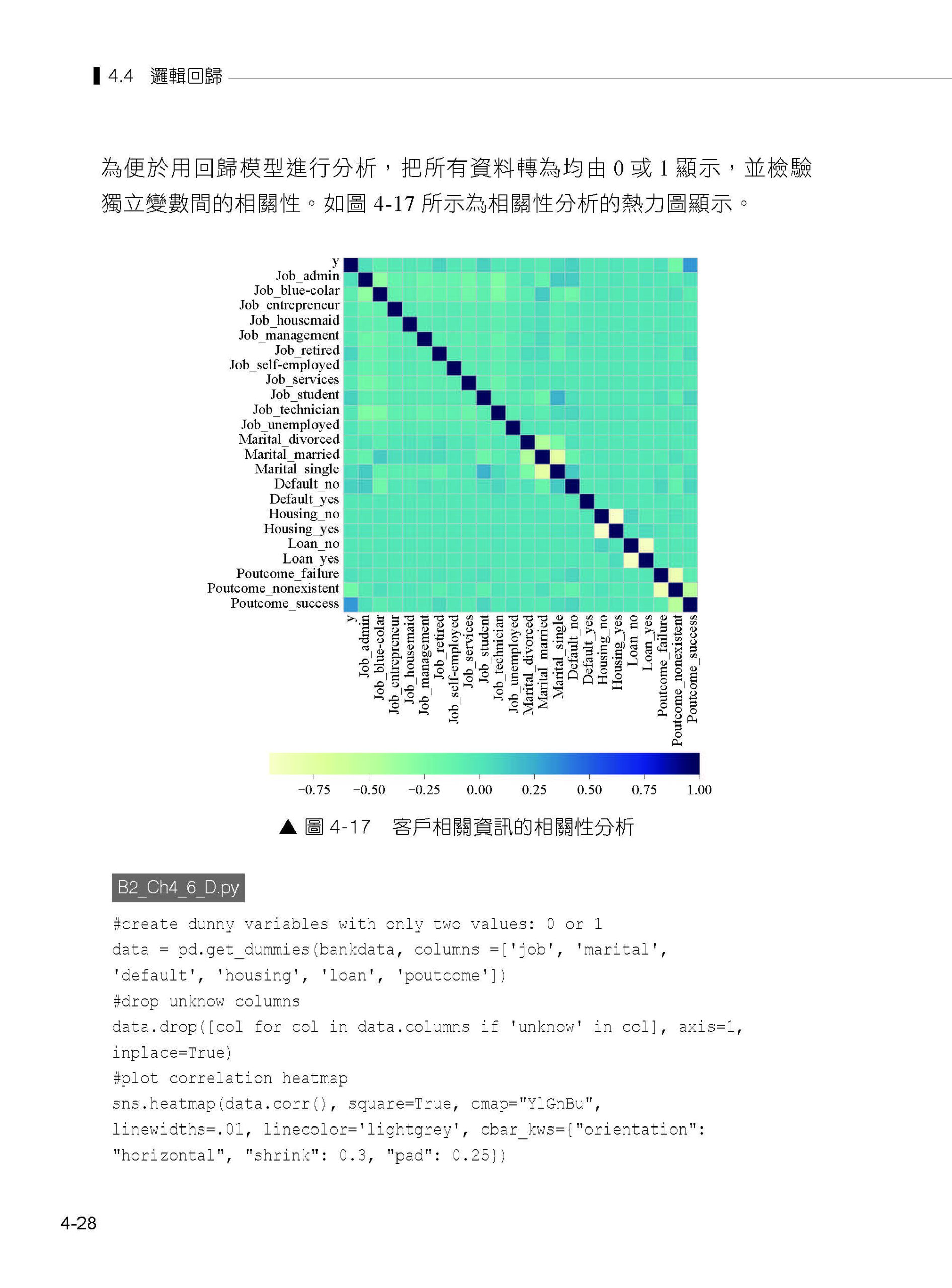
第4章 回歸分析 4.1 回歸分析概述 4.2 回歸模型的建模與評估 4.3 線性回歸 4.4 邏輯回歸 4.5 多項式回歸 4.6 嶺回歸 4.7 套索回歸
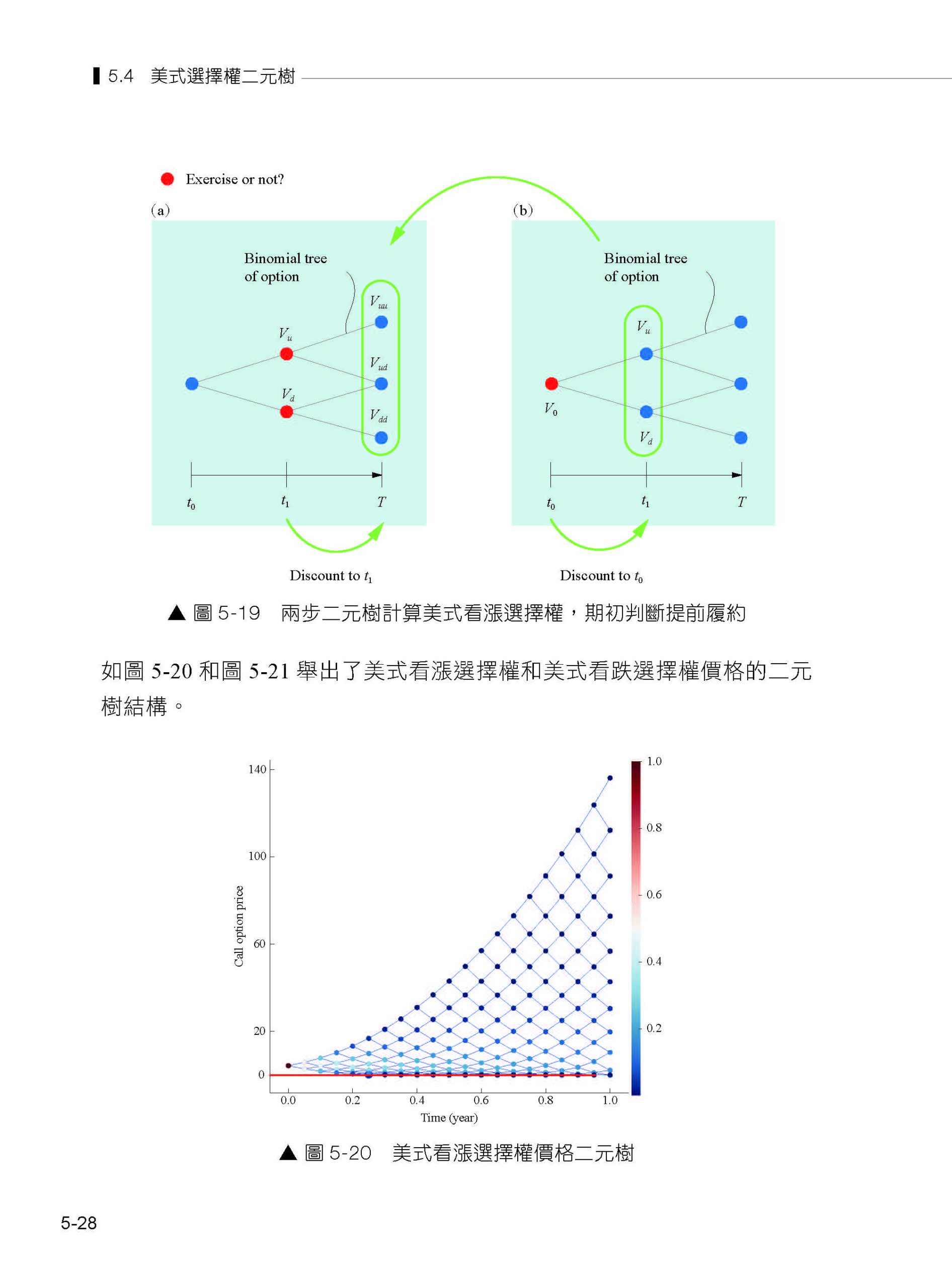
第5章 選擇權二元樹 5.1 選擇權市場 5.2 標的物二元樹 5.3 歐式選擇權二元樹 5.4 美式選擇權二元樹 5.5 二元樹步數影響 5.6 其他二元樹
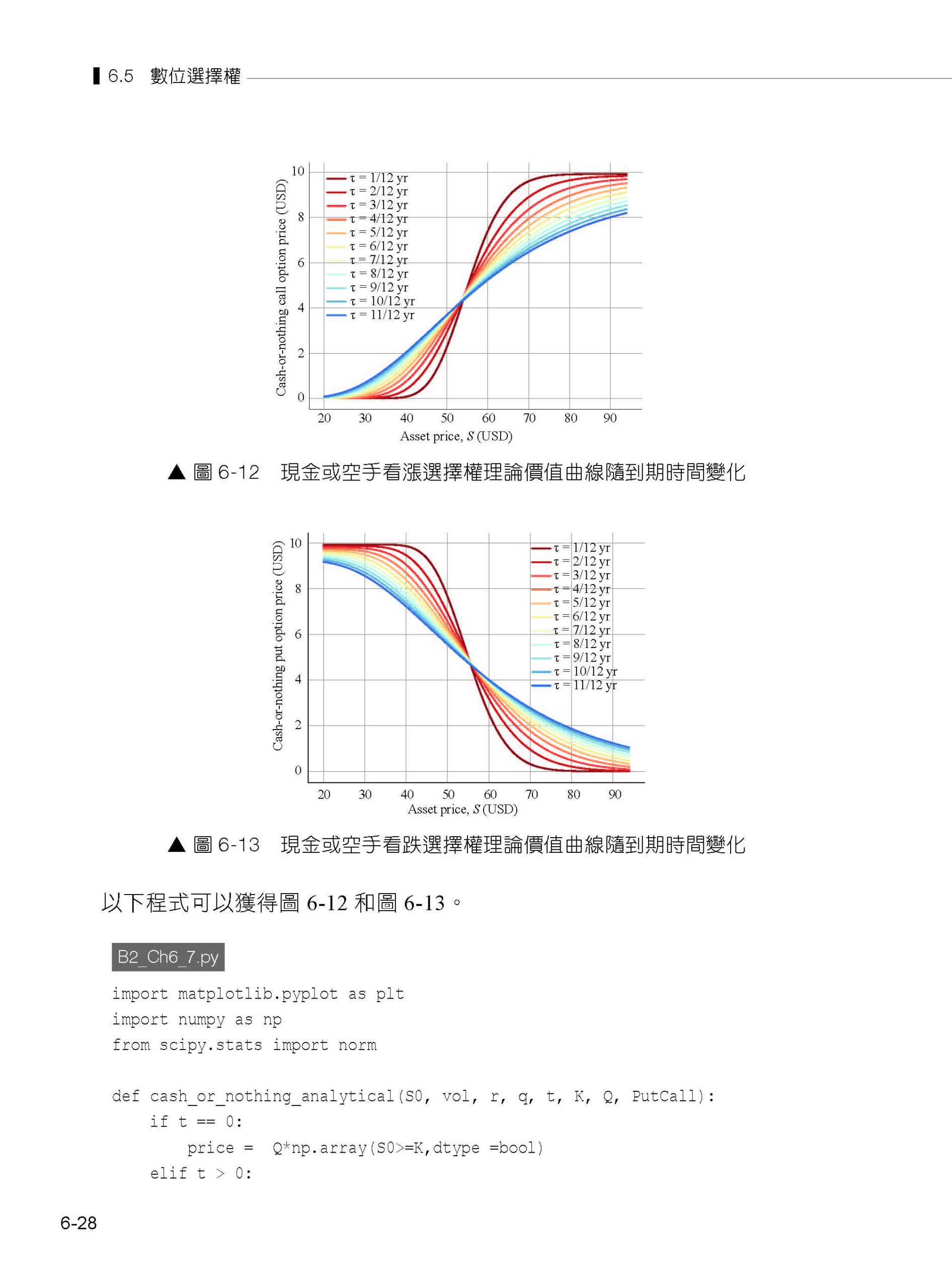
第6章 BSM選擇權定價 6.1 BSM模型 6.2 時間價值和內在價值 6.3 外匯選擇權 6.4 期貨選擇權和債券選擇權 6.5 數位選擇權
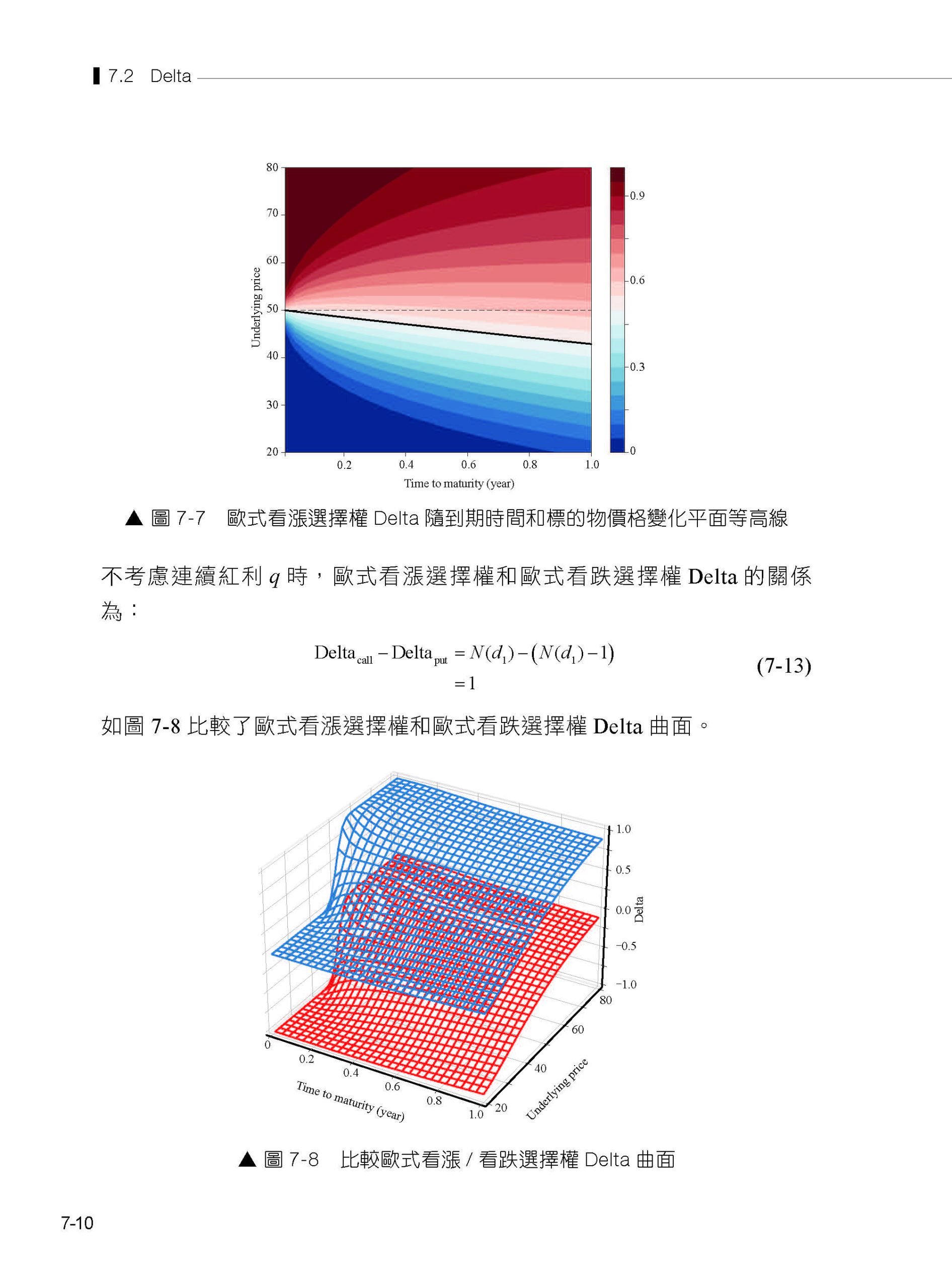
第7章 希臘字母 7.1 希臘字母 7.2 Delta 7.3 Gamma 7.4 Theta 7.5 Vega 7.6 Rho 230
第8章 市場風險 8.1 市場風險及其分類 8.2 市場風險度量 8.3 風險價值 8.4 參數法計算風險價值 8.5 歷史法計算風險價值 8.6 蒙地卡羅法計算風險價值
第9章 信用風險 9.1 信用風險的定義和分類 9.2 信用風險的度量 9.3 信用風險資料分析與處理 9.4 信用風險評分卡模型 9.5 信用評級機構 9.6 自展法求生存率 9.7 奧特曼Z分模型
第10章 交易對手信用風險 10.1 交易對手信用風險概念 10.2 交易對手信用風險度量 10.3 預期正曝露和最大潛在未來風險曝露 10.4 遠期合約的交易對手信用風險 10.5 利率互換的交易對手信用風險 10.6 貨幣互換的交易對手信用風險 10.7 交易對手信用風險緩釋 10.8 信用估值調整 10.9 錯向風險
第11章 投資組合理論Ⅰ 11.1 平均值方差理論 11.2 拉格朗日函數最佳化求解 11.3 整體最小風險資產組合 11.4 有效前端 11.5 有效前端實例 11.6 不可賣空有效前端
第12章 投資組合理論Ⅱ 12.1 包含無風險產品的投資組合 12.2 最佳風險投資組合及實例分析 12.3 無差別效用曲線 12.4 最佳完全投資組合實例分析 12.5 資產定價理論
備忘 |
序
| 人以「血」為「氣之母」。金融之於一個國家,猶如血液之於人的身體。風險管理作為必不可少的金融行業之一,時時刻刻都在管理著金融「血液」的流動,監控著金融「血液」的各項指標,是預防各類金融「血液」問題發生的重要管理方法。
現代金融風險管理是由西方世界在二戰以後系統性地提出、研究和發展起來的。一開始,還只是簡單地使用保險產品來避開個人或企業由於意外事件而遭受的損失。到了20 世紀50 年代,此類保險產品不僅難以面面俱到而且費用昂貴,風險管理開始以其他的形式出現。舉例來說,利用金融衍生品來管理風險,並在70 年代開始嶄露頭角,至80 年代已風靡全球。到90 年代,金融機構開始開發內部的風險管理模型,全球性的風險監管陸續介入並扮演起管理者的角色。如今,風險管理在不斷改善過程中,已經成為各金融機構的必備職能部門,在有效地分析、理解和管理風險的同時,也創造了大量的就業機會。
金融風險管理的進化還與量化金融的發展息息相關。量化金融最大的特點就是利用模型來解釋金融活動和現象,並對未來進行合理的預測。1827 年,當英國植物學家羅伯特•布朗 (Robert Brown) 盯著水中做無規則運動的花粉顆粒時,他不會想到幾十年後的1863年,法國人朱爾斯•雷諾特(Jules Regnault) 根據自己多年股票經紀人的經驗,第一次提出股票價格也服從類似的運動。到了1990 年,法國數學家路易士•巴切里爾(Louis Bachelier) 發表了博士論文《投機理論》The theory of speculation。從此,布朗運動被正式引入和應用到了金融領域,樹立了量化金融史上的首座里程碑。
而同樣歷史性的時刻,直到1973 年和1974 年才再次出現。美國經濟學家費希爾•布萊克 (Fischer Black)、邁倫•斯科爾斯 (Myron Scholes) 和羅伯特•默頓 (Robert Merton) 分別於這兩年提出並建立了Black-Scholes-Merton模型。該模型不僅實現了對選擇權產品的定價,其思想和方法還被拓展應用到了其他的各類金融產品和領域中,影響極其深遠。除了對隨機過程的應用,量化金融更是將各類統計模型、時間序列模型、數值計算技術等五花八門的神兵利器都招致麾下,大顯其威。而這些廣泛應用的模型、工具和方法,無疑都為金融風險管理提供了巨大的養分和能量,也成為了金融風險管理的重要手段。舉例來說,損益分佈、風險價值(VaR)、波動率、投資組合、風險對沖、違約機率、信用評級等重要的概念,就是在這肥沃的土壤上結出的果實。
金融風險管理師 (FRM) 就是在這樣的大背景下應運而生的國際專業資質認證。本叢書以FRM 為中心介紹實際工作所需的金融風險建模和管理知識,並且將Python 程式設計有機地結合到內容中。就形式而言,本書一大特點是透過豐富多彩的圖表和生動貼切的實例,深入淺出地將煩瑣的金融概念和複雜的計算結果進行了視覺化,能有效地幫助讀者領會重點並提高程式設計水準。
貿易戰、金融戰、貨幣戰這些非傳統意義的戰爭,雖不見炮火硝煙,但所到之處卻是哀鴻遍野。安得廣廈千萬間,風雨不動安如山。筆者希望本書系列,能為推廣金融風險管理的知識盡一份微薄之力,為從事該行業的讀者提供一點助益。在這變幻莫測的全球金融浪潮裡,為一方平安保駕護航,為盛世永駐盡心盡力。在這裡,筆者衷心地感謝清華大學出版社的欒大成老師,以及其他幾位 編輯老師對本叢書的大力支持,感謝身邊好友們的傾情協助和辛苦工作。最後,借清華大學校訓和大家共勉—天行健,君子以自強不息;地勢坤,君子以厚德載物。
✤ 致謝 謹以此書獻給我們的父母親。 |