描述
內容簡介
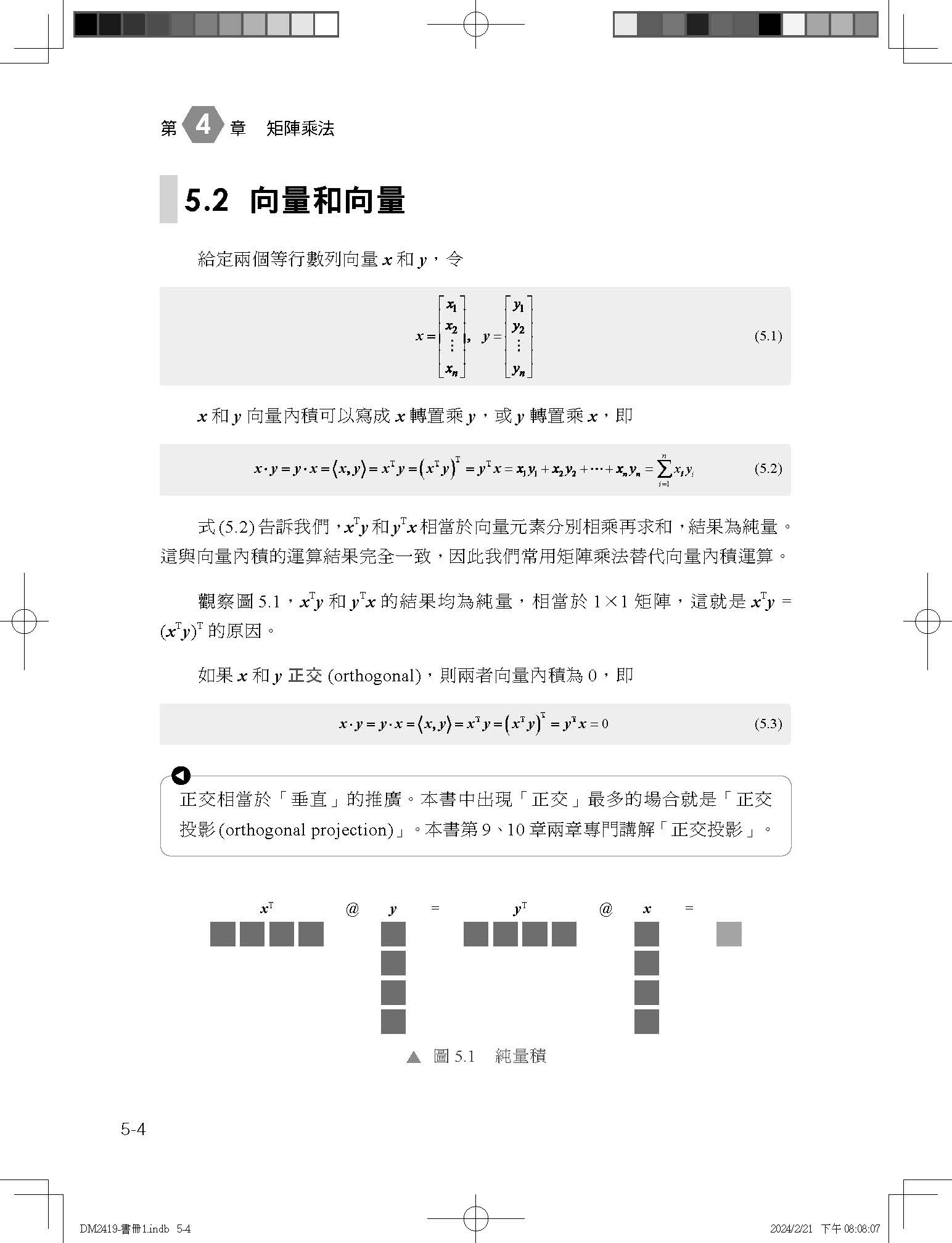
| !有資料就有矩陣,有矩陣就有向量,有向量就有幾何,有幾何就有空間
!從資料一路提升到張量的所有數學基礎 !將數學視為思想、工具、語言、體系、基石、藝術的角度進行學習 !分為向量、矩陣、向量空間、矩陣分解、微積分、空間幾何、資料 !所有機器學習、深度學習最重要的基礎數學概念 !不再亂猜,寫機器學習程式碼時,每行指令背後代表的數學基礎 !學矩陣就是學AI,從此看到AI程式碼完全無負擔 AI熱潮來臨,每個人都很怕直接被機器取代,不管文科理科背景的人,每個人都想搭上AI快車飛速到達未來。然而你的第一關就是數學。數學是宇宙的共同語言,也是人類意志極緻的展現。數學從數字開始進入高維之後,向量、矩陣、張量將整個人類文明帶入新的境界,也將我們的世界從點線面體推向無法視覺化的高維空間,而針對空間的運算,更是所有科學的重要基礎。空間幾何這門完全和生活知識抽離的學科,看似是和向量打交道而已,但卻是整個世界運行的基礎,近年AI興起,機器學習及深度學習成為熱門行業,當你想要學習TensorFlow時,面對的第一個觀念就是張量(Tensor)。這些名詞讓你感到陌生又不是完全不認識時,就是重拾矩陣的時候了。本書利用最小的成本,幫你把這個又陌生又熟悉的老朋友重新交往。作者從最簡單的加法開始說明,一直到機器學習中的梯度、偏導數、積分、矩陣、線性代數,從小學到研究所所學的數學,一一在適當的章節出現,當你讀到某個章節時,會發現「啊!原來如此,這就是奇異值分解在機器學習的原理啊!」,有一種豁然開朗的感覺,相信這種驚喜在全書中會不斷出現。ChatGPT出來之後,AI已經光速啟動,有志加入這個行業,也只能快速跟上,而這本書,正是你進入的最佳助手,與其繼續逃避直到被淘汰,不如就花一點時間,把這本本來就不難的書看完,補上你個人AI志業的最重要一塊拼圖。 全書分為以下幾個部分:向量:從資料、矩陣、向量、幾何、空間開始談起,包括向量運算,範數等基本定理。接下來談到矩陣,把矩陣所有的性質(四則運算、表格、秩等)說明清楚,更有重要的內外積等。第三部分談的是向量,包括座標系、各種變換、維度、行列視,投影、正交、基等性質。第四部分談的是矩陣分解,實作了包括LU、Cholesky、QR,特徵/奇異值分解。第五部分就是談到空間的微積分,如多元函式、偏導、梯度、方向微分、泰勒展開等。也說明了拉格朗日乘子等。第六部分說明了空間幾何,包括直線、超平面、圓錐曲線等。也說明了曲面和正定性等問題。最後一部分則整理了前面所有觀念,發展至資料統計、SVD分解、機器學習、線性迴歸及PCA原理。搭配本書系其它書籍,相信AI的數學,對你來說只會是開心而不是阻礙。 |
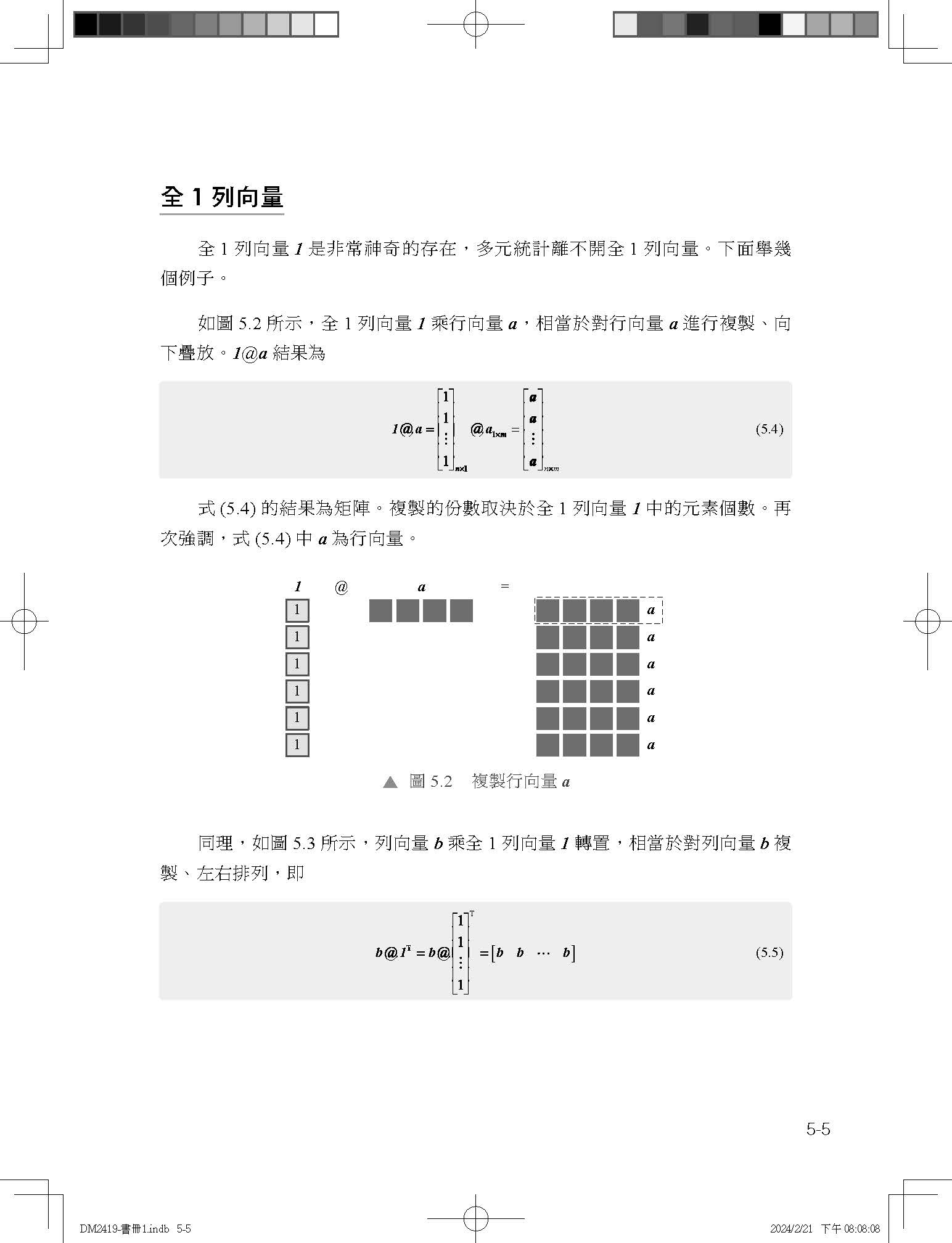
作者簡介
| 姜偉生,博士FRM。勤奮的小鎮做題家,熱愛知識可視化和開源分享。自2022年8月開始,在GitHub上開源「鳶尾花書」學習資源,截至2023年9月,已經分享4000多頁PDF、4000多幅矢量圖、約2000個代碼文件,全球讀者數以萬計。 |
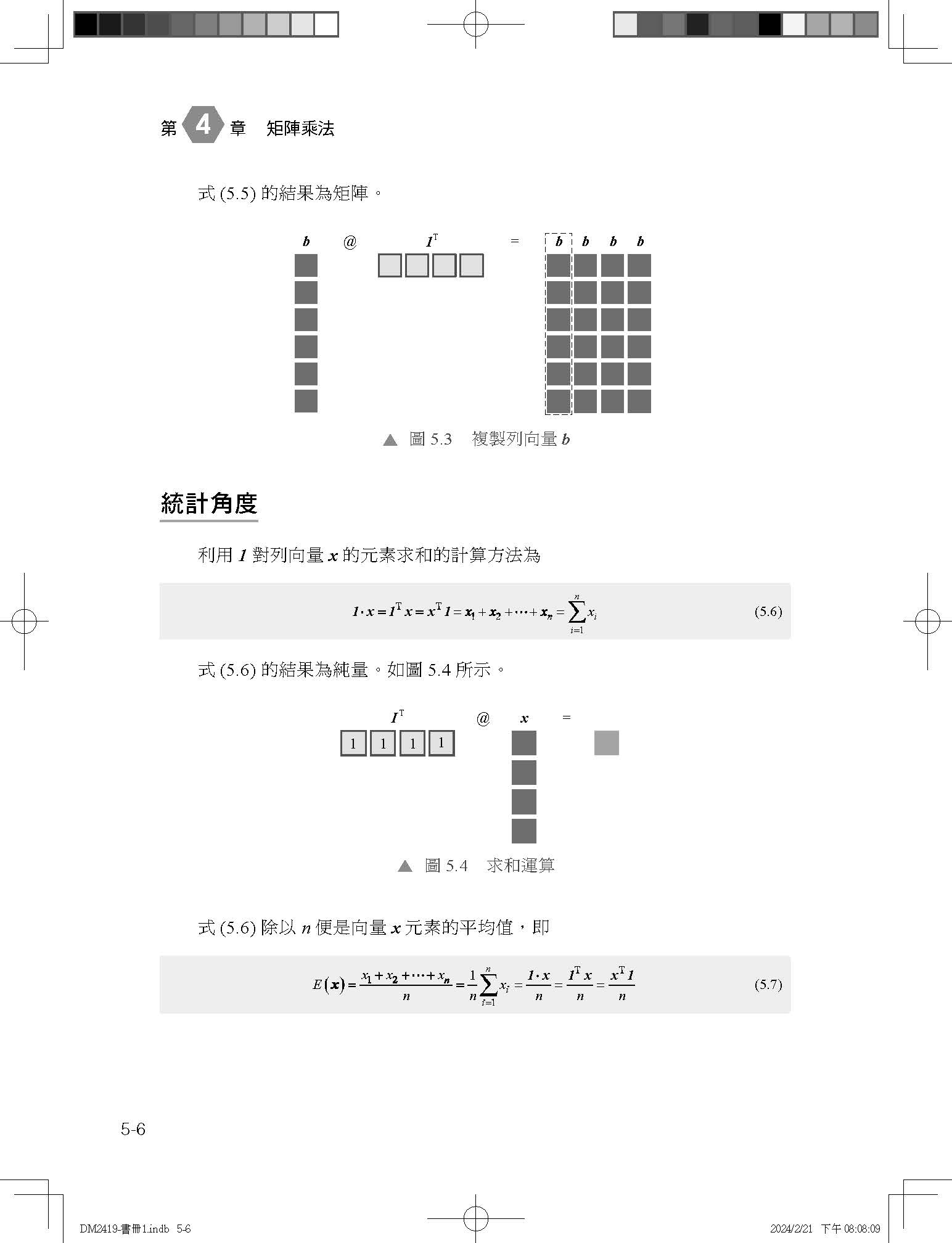
目錄
| 第 1章 不止向量
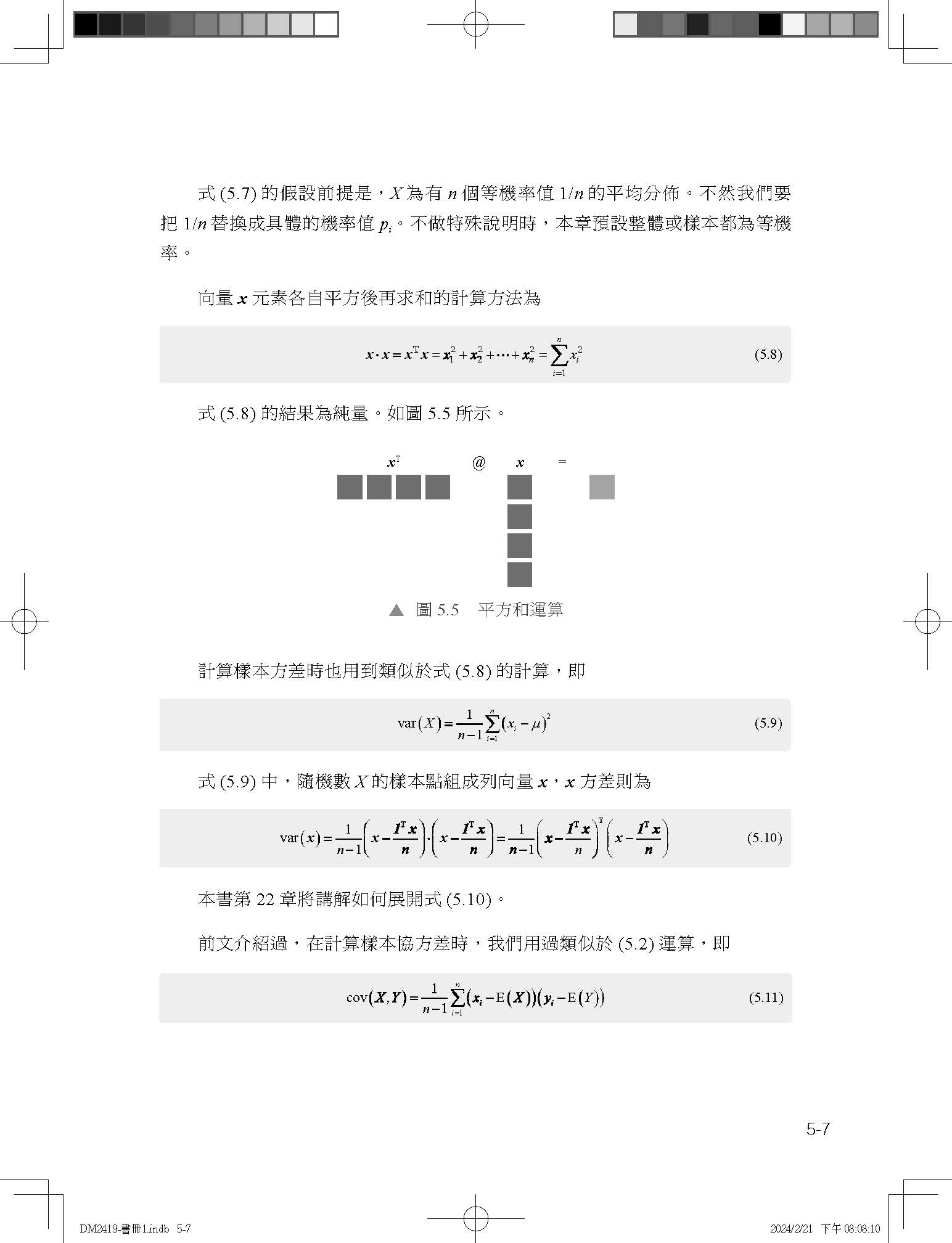
1.1 有資料的地方,必有矩陣 1.2 有矩陣的地方,更有向量 1.3 有向量的地方,就有幾何 1.4 有幾何的地方,皆有空間 1.5 有資料的地方,定有統計
第 2章 向量運算 2.1 向量:多面手 2.2 行向量、列向量 2.3 向量長度:模,歐氏距離,L2範數 2.4 加減法:對應位置元素分別相加減 2.5 純量乘法:向量縮放 2.6 向量內積:結果為純量 2.7 向量夾角:反餘弦 2.8 餘弦相似度和餘弦距離 2.9 向量積:結果為向量 2.10 逐項積:對應元素分別相乘 2.11 張量積:張起網格面
第 3章 向量範數 3.1 Lp範數:L2範數的推廣 3.2 Lp範數和超橢圓的聯繫 3.3 L1範數:旋轉正方形 3.4 L2範數:正圓 3.5 L∞範數:正方形 3.6 再談距離度量
第4章 矩陣 4.1 矩陣:一個不平凡的表格 4.2 矩陣形狀:每種形狀都有特殊用途 4.3 基本運算:加減和純量乘法 4.4 廣播原則 4.5 矩陣乘法:線性代數的運算核心 4.6 兩個角度解剖矩陣乘法 4.7 轉置:繞主對角線鏡像 4.8 矩陣逆:「相當於 」除法運算 4.9 跡:主對角元素之和 4.10 逐項積:對應元素相乘 4.11 行列式:將矩陣映射到純量值
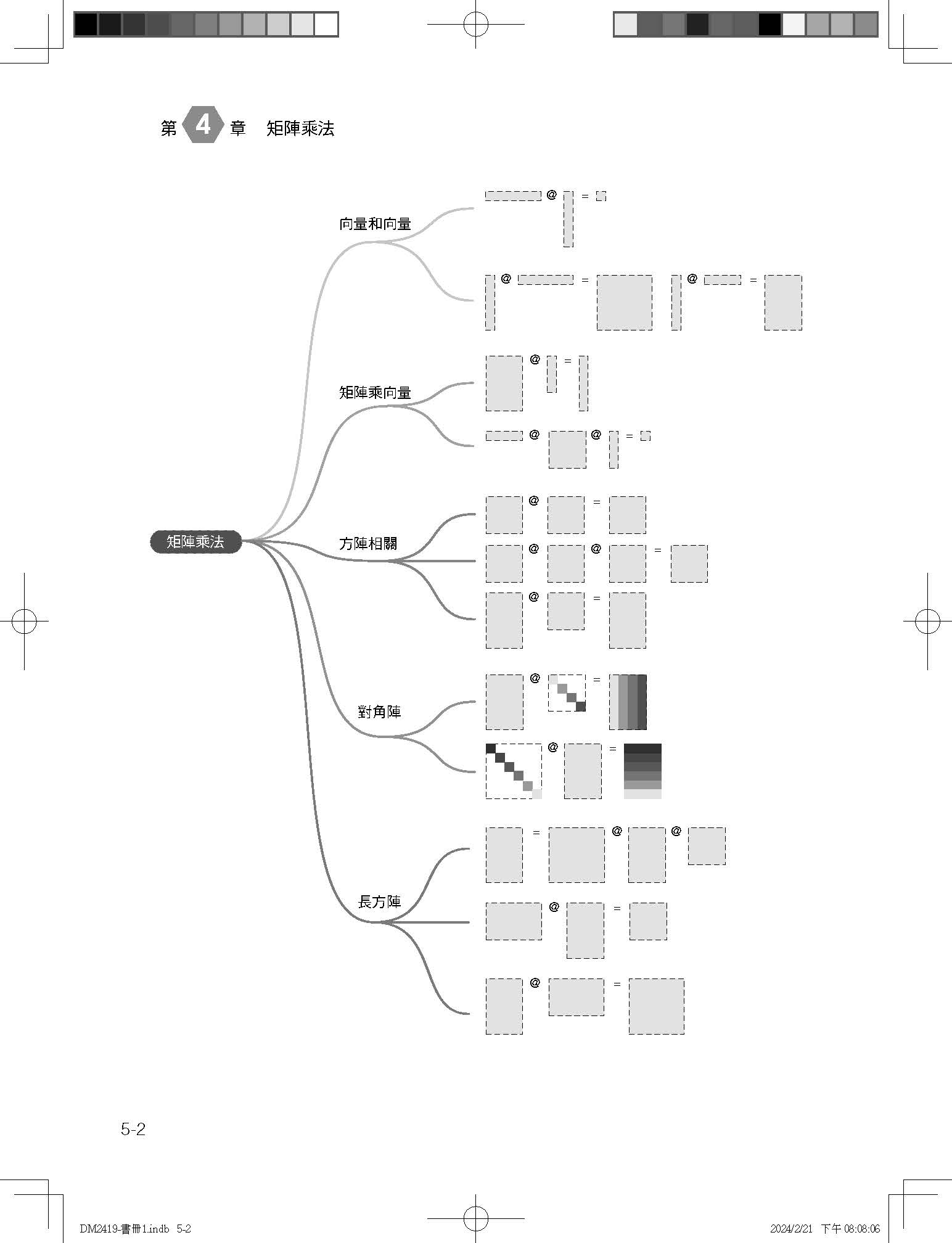
第5章 矩陣乘法 5.1 矩陣乘法:形態豐富多樣 5.2 向量和向量 5.3 再聊全1列向量 5.4 矩陣乘向量:線性方程式組 5.5 向量乘矩陣乘向量:二次型 5.6 方陣次方陣:矩陣分解 5.7 對角陣:批次縮放 5.8 置換矩陣:調換元素順序 5.9 矩陣乘向量:映射到一維 5.10 矩陣乘矩陣:映射到多維 5.11 長方陣:奇異值分解、格拉姆矩陣、張量積 5.12 愛因斯坦求和約定 5.13 矩陣乘法的幾個雷區
第6章 分塊矩陣 6.1 分塊矩陣:橫平垂直切豆腐 6.2 矩陣乘法第一角度:純量積展開 6.3 矩陣乘法第二角度:外積展開 6.4 矩陣乘法更多角度:分塊多樣化 6.5 分塊矩陣的逆 6.6 克羅內克積:矩陣張量積
第 7章 向量空間 7.1 向量空間:從直角座標系說起 7.2 給向量空間塗顏色:RGB色卡 7.3 張成空間:線性組合紅、綠、藍三原色 7.4 線性無關:紅色和綠色,調不出青色 7.5 非正交基底:青色、品紅、黃色 7.6 基底轉換:從紅、綠、藍,到青色、品紅、黃色
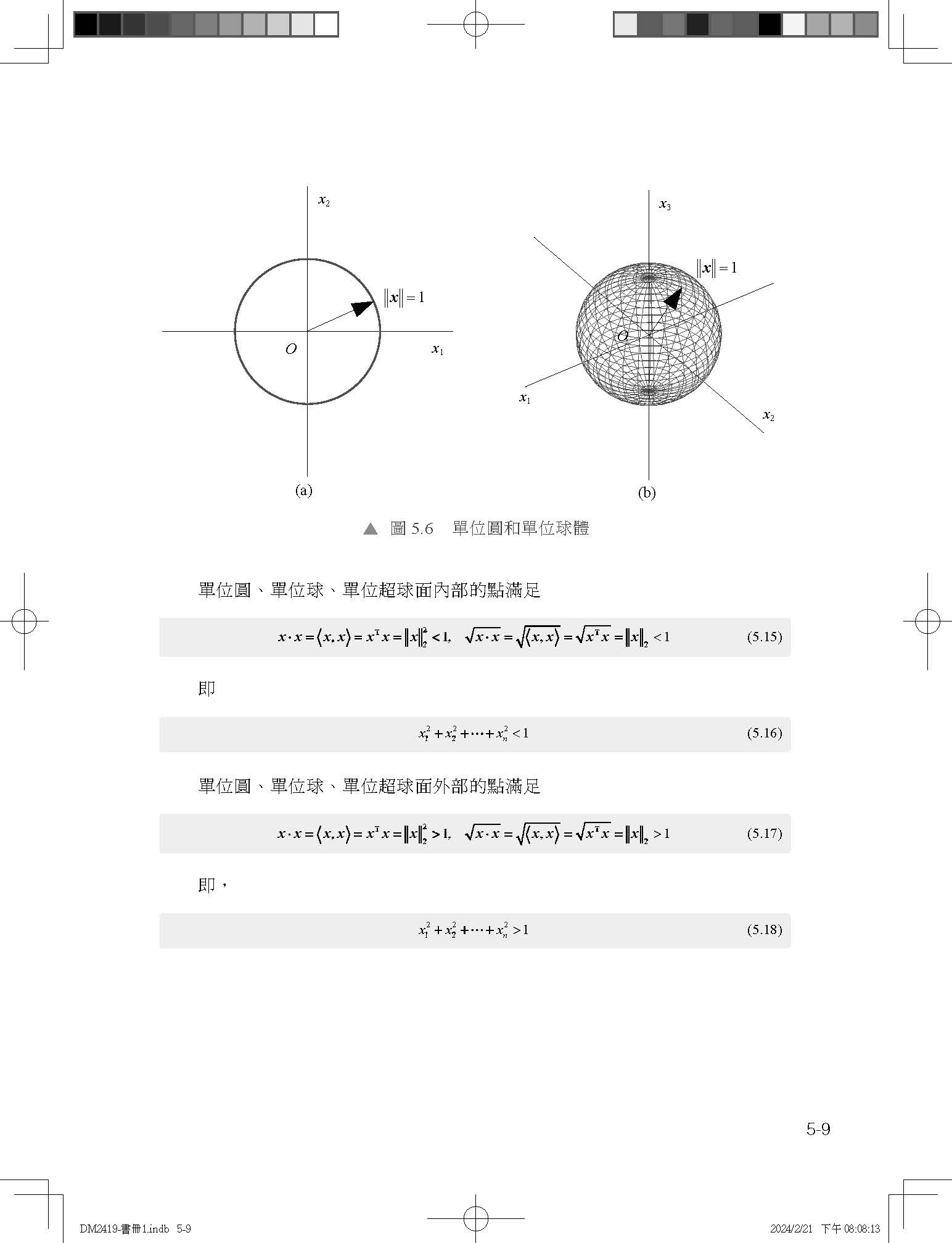
第8章 幾何變換 8.1 線性變換:線性空間到自身的線性映射 8.2 平移:仿射變換,原點變動 8.3 縮放:對角陣 8.4 旋轉:行列式值為1 8.5 鏡像:行列式值為負 8.6 投影:降維操作 8.7 再談行列式值:幾何角度
第 9章 正交投影 9.1 純量投影:結果為純量 9.2 向量投影:結果為向量 9.3 正交矩陣:一個規範正交基底 9.4 規範正交基底性質 9.5 再談鏡像:從投影角度 9.6 格拉姆-施密特正交化 9.7 投影角度看回歸
第 10 章 資料投影 10.1 從一個矩陣乘法運算說起 10.2 二次投影 + 層層疊加 10.3 二特徵資料投影:標準正交基底 10.4 二特徵資料投影:規範正交基底 10.5 四特徵資料投影:標準正交基底 10.6 四特徵資料投影:規範正交基底 10.7 資料正交化
第 11章 矩陣分解 11.1 矩陣分解:類似因式分解 11.2 LU分解:上下三角 11.3 Cholesky分解:適用於正定矩陣 11.4 QR分解:正交化 11.5 特徵值分解:刻畫矩陣映射的特徵 11.6 奇異值分解:適用於任何實數矩陣
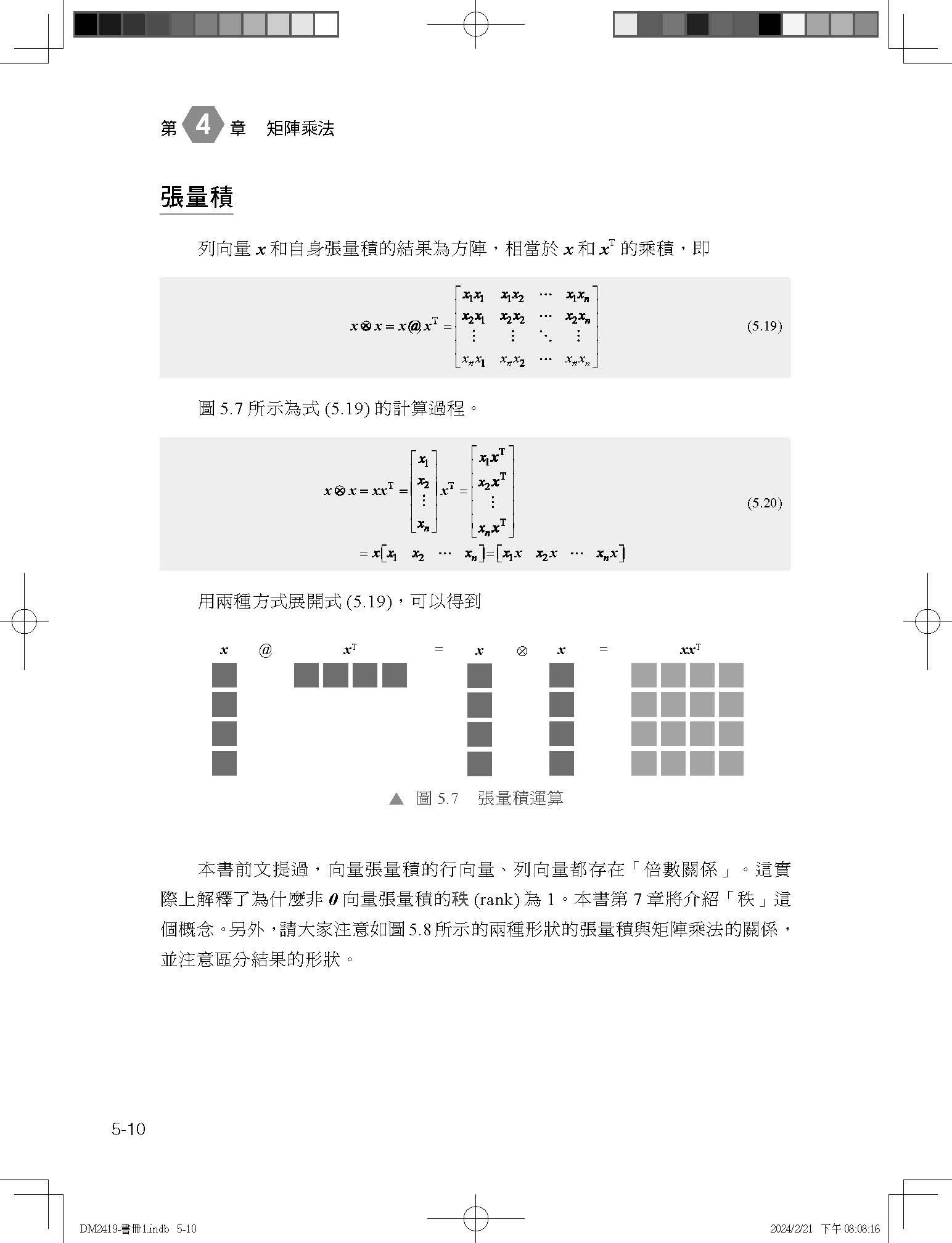
第 12章 Cholesky分解 12.1 Cholesky分解 12.2 正定矩陣才可以進行Cholesky分解 12.3 幾何角度:開合 12.4 幾何變換:縮放 → 開合 12.5 推廣到三維空間 12.6 從格拉姆矩陣到相似度矩陣
第 13章 特徵值分解 13.1 幾何角度看特徵值分解 13.2 旋轉 → 縮放 → 旋轉 13.3 再談行列式值和線性變換 13.4 對角化、譜分解 13.5 聊聊特徵值 13.6 特徵值分解中的複數現象
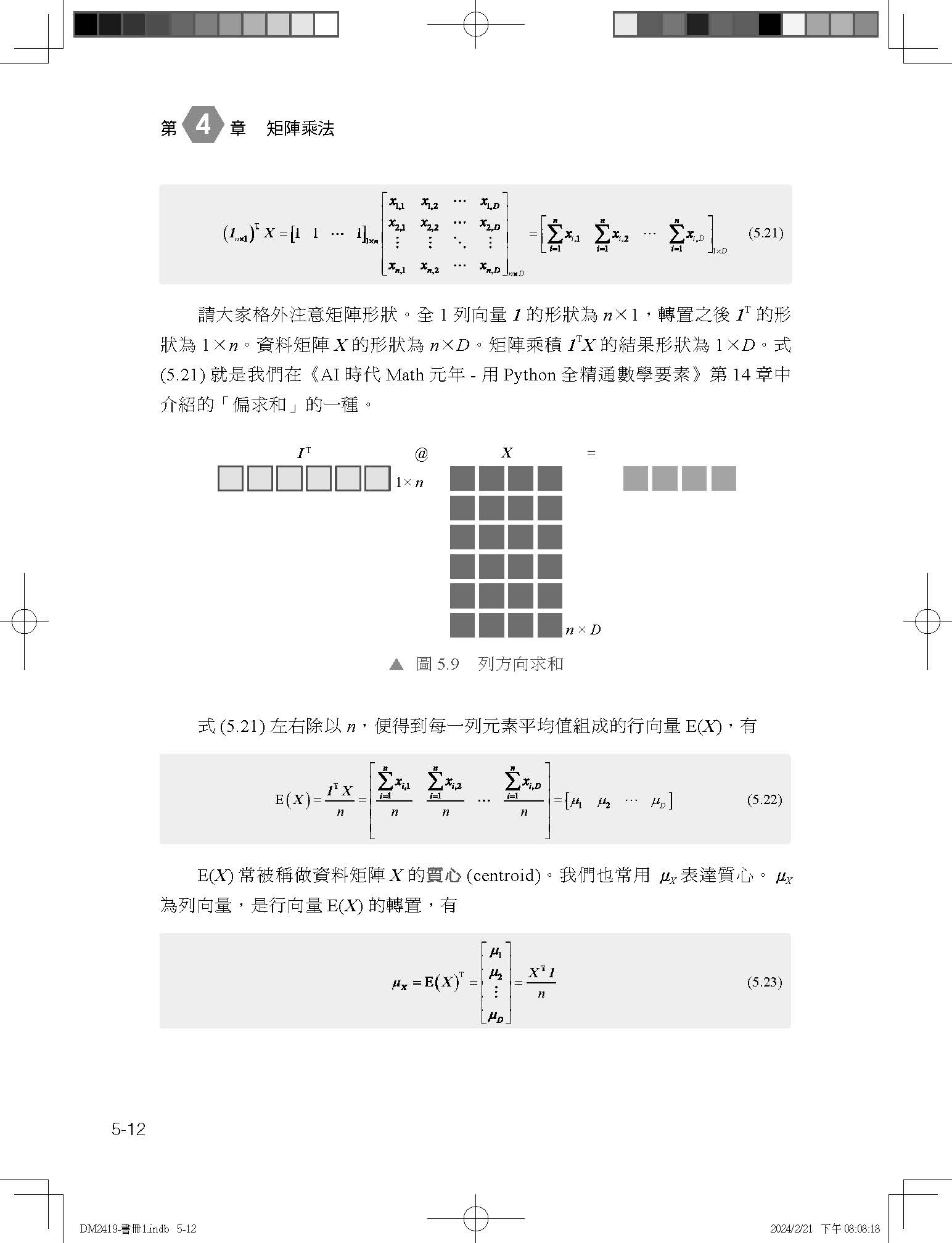
第 14章 深入特徵值分解 14.1 方陣開方 14.2 矩陣指數:冪級數的推廣 14.3 費氏數列:求通項式 14.4 馬可夫過程的平穩狀態 14.5 瑞利商 14.6 再談橢圓:特徵值分解
第 15章 奇異值分解 15.1 幾何角度:旋轉 → 縮放 → 旋轉 15.2 不同類型SVD分解 15.3 左奇異向量矩陣U 15.4 右奇異向量矩陣V 15.5 兩個角度:投影和資料疊加
第 16章 深入奇異值分解 16.1 完全型:U為方陣 16.2 經濟型:S去掉零矩陣,變方陣 16.3 緊湊型:非滿秩 16.4 截斷型:近似 16.5 資料還原:層層疊加 16.6 估計與誤差:截斷型SVD 16.7 正交投影:資料正交化
第 17章 多元函式微分 17.1 偏導:特定方向的變化率 17.2 梯度向量:上山方向 17.3 法向量:垂直於切平面 17.4 方向性微分:函式任意方向的變化率 17.5 泰勒展開:一元到多元
第 18章 拉格朗日乘子法 18.1 回顧最佳化問題 18.2 等式約束條件 18.3 線性等式約束 18.4 非線性等式約束 18.5 不等式約束 18.6 再談特徵值分解:最佳化角度 18.7 再談SVD:最佳化角度 18.8 矩陣範數:矩陣 → 純量,矩陣「大小 」 18.9 再談資料正交投影:最佳化角度
第 19章 直線到超平面 19.1 切向量:可以用來定義直線 19.2 法向量:定義直線、平面、超平面 19.3 超平面:一維直線和二維平面的推廣 19.4 平面與梯度向量 19.5 中垂線:用向量求解析式 19.6 用向量計算距離
第 20 章 再談圓錐曲線 20.1 無處不在的圓錐曲線 20.2 正圓:從單位圓到任意正圓 20.3 單位圓到旋轉橢圓:縮放 → 旋轉 → 平移 20.4 多元高斯分佈:矩陣分解、幾何變換、距離 20.5 從單位雙曲線到旋轉雙曲線 20.6 切線:建構函式,求梯度向量 20.7 法線:法向量垂直於切向量
第 21章 曲面和正定性 21.1 正定性 21.2 幾何角度看正定性 21.3 開口朝上抛物面:正定 21.4 山谷面:半正定 21.5 開口朝下抛物面:負定 21.6 山脊面:半負定 21.7 雙曲抛物面:不定 21.8 多極值曲面:局部正定性
第 22章 資料與統計 22.1 統計 + 線性代數:以鳶尾花資料為例 22.2 平均值:線性代數角度 22.3 質心:平均值排列成向量 22.4 中心化:平移 22.5 分類資料:加標籤 22.6 方差:平均值向量沒有解釋的部分 22.7 協方差和相關性係數 22.8 協方差矩陣和相關性係數矩陣
第 23章 資料空間 23.1 從資料矩陣X說起 23.2 向量空間:從SVD分解角度理解 23.3 緊湊型SVD分解:剔除零空間 23.4 幾何角度說空間 23.5 格拉姆矩陣:向量模、夾角餘弦值的集合體 23.6 標準差向量:以資料質心為起點 23.7 白話說空間:以鳶尾花資料為例
第 24章 資料分解 24.1 為什麼要分解矩陣? 24.2 QR分解:獲得正交系 24.3 Cholesky分解:找到列向量的座標 24.4 特徵值分解:獲得行空間和零空間 24.5 SVD分解:獲得四個空間
第 25章 資料應用 25.1 從線性代數到機器學習 25.2 從隨機變數的線性變換說起 25.3 單方向映射 25.4 線性回歸 25.5 多方向映射 25.6 主成分分析 |
序
| Preface
前言
感謝 首先感謝大家的信任。 作者僅是在學習應用資料科學和機器學習演算法時,多讀了幾本數學書,多做了一些思考和知識 整理而已。知者不言,言者不知。知者不博,博者不知。由於作者水準有限,斗膽把自己所學所思與大家分享,作者權當無知者無畏。希望大家在Github多提意見,讓這套書成為作者和讀者共同參與創作的作品。 特別感謝清華大學出版社的欒大成老師。從選題策劃、內容創作到裝幀設計,欒老師事無巨細、一路陪伴。每次與欒老師交流,都能感受到他對優質作品的追求、對知識分享的熱情。
出來混總是要還的 曾經,考試是我們學習數學的唯一動力。考試是頭懸樑的繩,是錐刺股的錐。我們中的大多數人 從小到大為各種考試埋頭題海,數學味同嚼蠟,甚至讓人恨之入骨。 數學所帶來了無盡的「折磨」。 我們甚至恐懼數學,憎恨數學,恨不得一走出校門就把數學拋之腦後,老死不相往來。 可悲可笑的是,我們很多人可能會在畢業的五年或十年以後,因為工作需要,不得不重新學習微積分、線性代數、機率統計,悔恨當初沒有學好數學,甚至遷怒於教材和老師。 這一切不能都怪數學,值得反思的是我們學習數學的方法和目的。
再給自己一個學數學的理由 為考試而學數學,是被逼無奈的舉動。而為數學而數學,則又太過高尚而遙不可及。 相信對絕大部分的我們來說,數學是工具、是謀生手段,而非目的。我們主動學數學,是想用數學工具解決具體問題。 現在,這套書給大家一個「學數學、用數學」的全新動力—資料科學、機器學習。 資料科學和機器學習已經深度融合到我們生活的各方面,而數學正是開啟未來大門的鑰匙。不是所有人生來都握有一副好牌,但是掌握「數學 + 程式設計 + 機器學習」的知識絕對是王牌。這次,學習數學不再是為了考試、分數、升學,而是投資時間、自我實現、面向未來。未來已來,你來不來?
本套書系如何幫到你 為了讓大家學數學、用數學,甚至愛上數學,作者可謂頗費心機。在創作這套書時,作者儘量克服傳統數學教材的各種弊端,讓大家學習時有興趣、看得懂、有思考、更自信、用得著。
為此,叢書在內容創作上突出以下幾個特點。
數學 + 藝術 全圖解,極致視覺化,讓數學思想躍然紙上、生動有趣、一看就懂,同時提高大家的資料思維、幾何想像力、藝術感。 零基礎 從零開始學習Python程式設計,從寫第一行程式到架設資料科學和機器學習應用,儘量將陡峭學習曲線拉平。 知識網路 打破數學板塊之間的門檻,讓大家看到數學代數、幾何、線性代數、微積分、 機率統計等板塊之間的聯繫,編織一張綿密的數學知識網路。 動手 授人以魚不如授人以漁,和大家一起寫程式、創作數學動畫、互動App。 學習生態 構造自主探究式學習生態環境「紙質圖書 + 程式檔案 + 視覺化工具 + 思維導圖」 ,提供各種優質學習資源。 理論 + 實踐 從加減乘除到機器學習,叢書內容安排由淺入深、螺旋上升,兼顧理論和實 踐;在程式設計中學習數學,學習數學時解決實際問題。
雖然本書標榜「從加減乘除到機器學習」, 但是建議讀者朋友們至少具備高中數學知識。如果讀者正在學習或曾經學過大學數學 (微積分、線性代數、機率統計) ,這套書就更容易讀懂了。
聊聊數學 數學是工具。錘子是工具,剪刀是工具,數學也是工具。
數學是思想。數學是人類思想高度抽象的結晶體。在其冷酷的外表之下,數學的核心實際上就是人類樸素的思想。學習數學時,知其然,更要知其所以然。不要死記硬背公式定理,理解背後的數學思想才是關鍵。如果你能畫一幅圖、用簡單的語言描述清楚一個公式、一則定理,這就說明你真正理解了它。
數學是語言。就好比世界各地不同種族有自己的語言,數學則是人類共同的語言和邏輯。數學這門語言極其精準、高度抽象,放之四海而皆準。雖然我們中大多數人沒有被數學「女神」選中,不能 為人類對數學認知開疆擴土;但是,這絲毫不妨礙我們使用數學這門語言。就好比,我們不會成為語言學家,我們完全可以使用母語和外語交流。
數學是系統。代數、幾何、線性代數、微積分、機率統計、最佳化方法等,看似一個個孤島,實際上都是數學網路的一條條織線。建議大家學習時,特別關注不同數學板塊之間的聯繫,見樹,更要見林。
數學是基石。拿破崙曾說「數學的日臻完善和國強民富息息相關。」數學是科學進步的根基,是經濟繁榮的支柱,是保家衛國的武器,是探索星辰大海的航船。
數學是藝術。數學和音樂、繪畫、建築一樣,都是人類藝術體驗。透過視覺化工具,我們會在看似枯燥的公式、定理、資料背後,發現數學之美。
數學是歷史,是人類共同記憶體。「歷史是過去,又屬於現在,同時在指引未來。」數學是人類的集體學習思考,它把人的思維符號化、形式化,進而記錄、累積、傳播、創新、發展。從甲骨、泥板、石板、竹簡、木牘、紙草、羊皮卷冊、活字印刷、紙質書,到數字媒介,這一過程持續了數千年,至今綿延不息。
數學是無窮無盡的想像力,是人類的好奇心,是自我挑戰的毅力,是一個接著一個的問題,是看似荒誕不經的猜想,是一次次膽大包天的批判性思考,是敢於站在前人臂膀之上的勇氣,是孜孜不倦 地延展人類認知邊界的不懈努力。
家園、詩、遠方 諾瓦利斯曾說:「哲學就是懷著一種鄉愁的衝動到處去尋找家園。」 在紛繁複雜的塵世,數學純粹得就像精神的世外桃源。數學是,一束光,一條巷,一團不滅的希望,一股磅礴的力量,一個值得寄託的避風港。 打破陳腐的鎖鏈,把功利心暫放一邊,我們一道懷揣一份鄉愁,心存些許詩意,踩著藝術維度,投入數學張開的臂膀,駛入它色彩斑斕、變幻無窮的深港,感受久違的歸屬,一睹更美、更好的遠方。 |