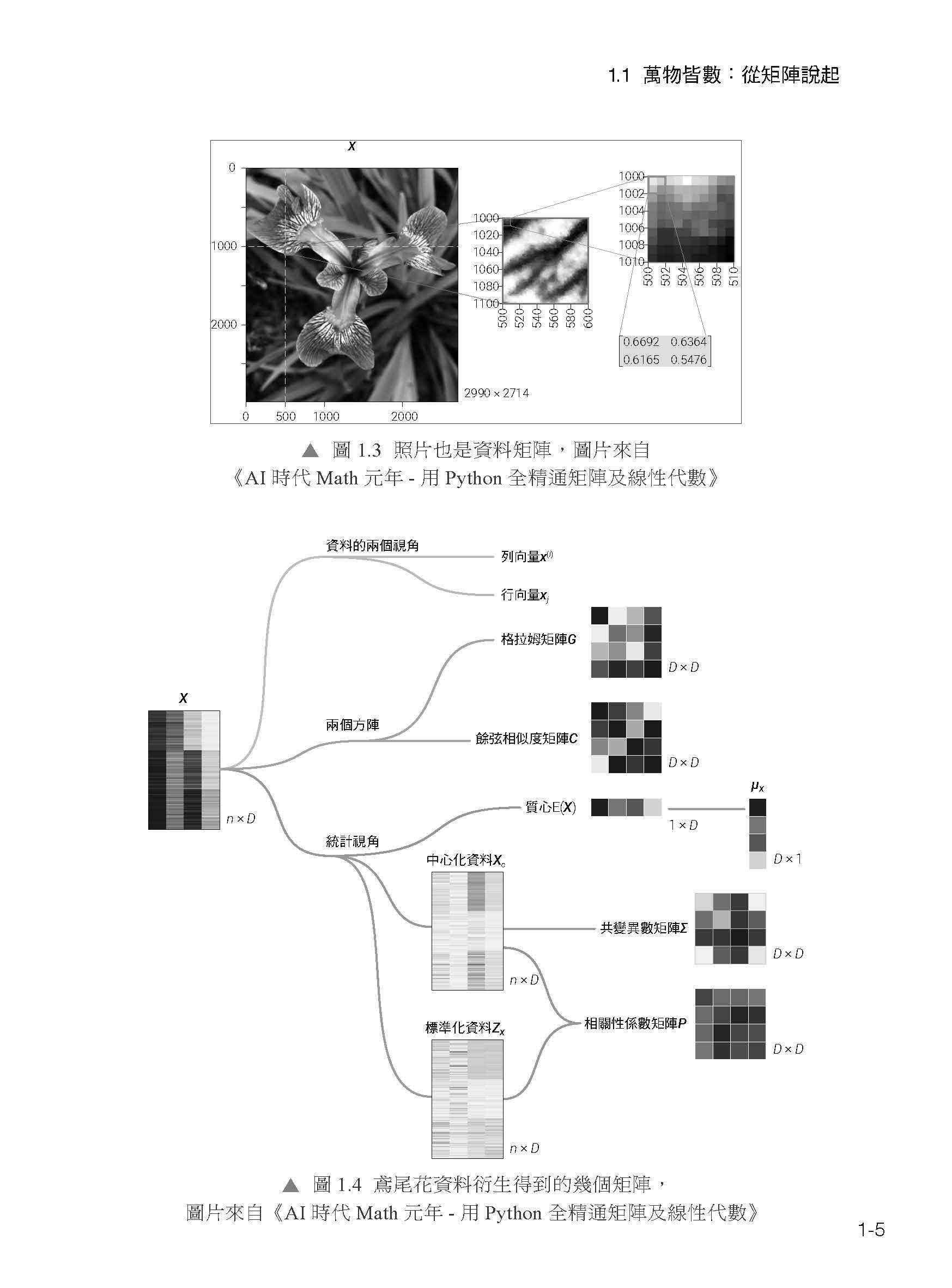
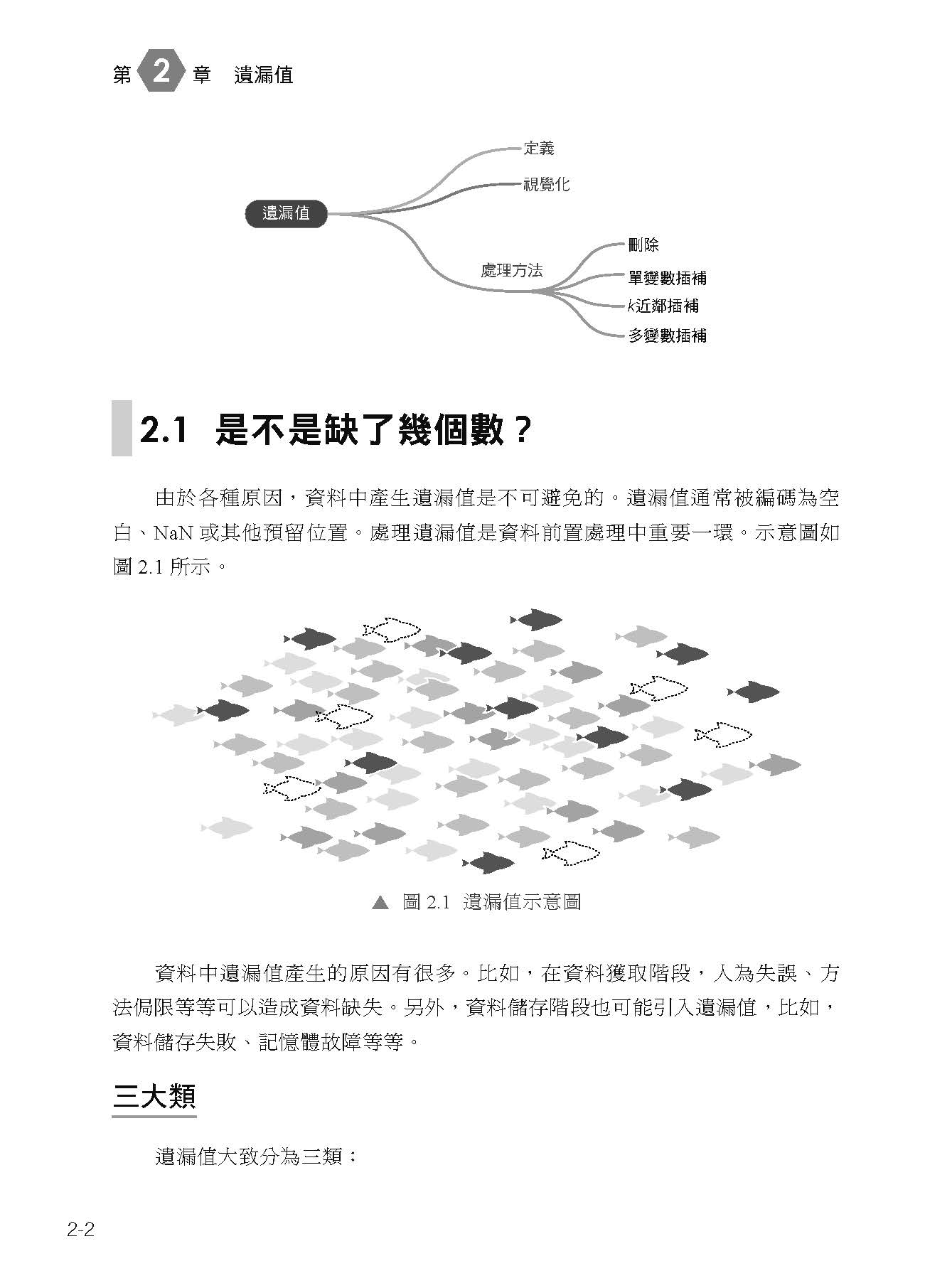
描述
內容簡介
|
作者簡介
| 姜偉生
博士FRM。勤奮的小鎮做題家,熱愛知識可視化和開源分享。自2022年8月開始,在GitHub上開源「鳶尾花書」學習資源,截至2023年9月,已經分享4000多頁PDF、4000多幅矢量圖、約2000個代碼文件,全球讀者數以萬計。目前著有《手術刀般精準的FRM:用Python科學管控財金風險》,及「鳶尾花數學大系:從加減乘除到機器學習」叢書7冊,此書系授權台灣深智數位出版社譯著繁體中文版。 |
目錄
| 第1篇 綜述
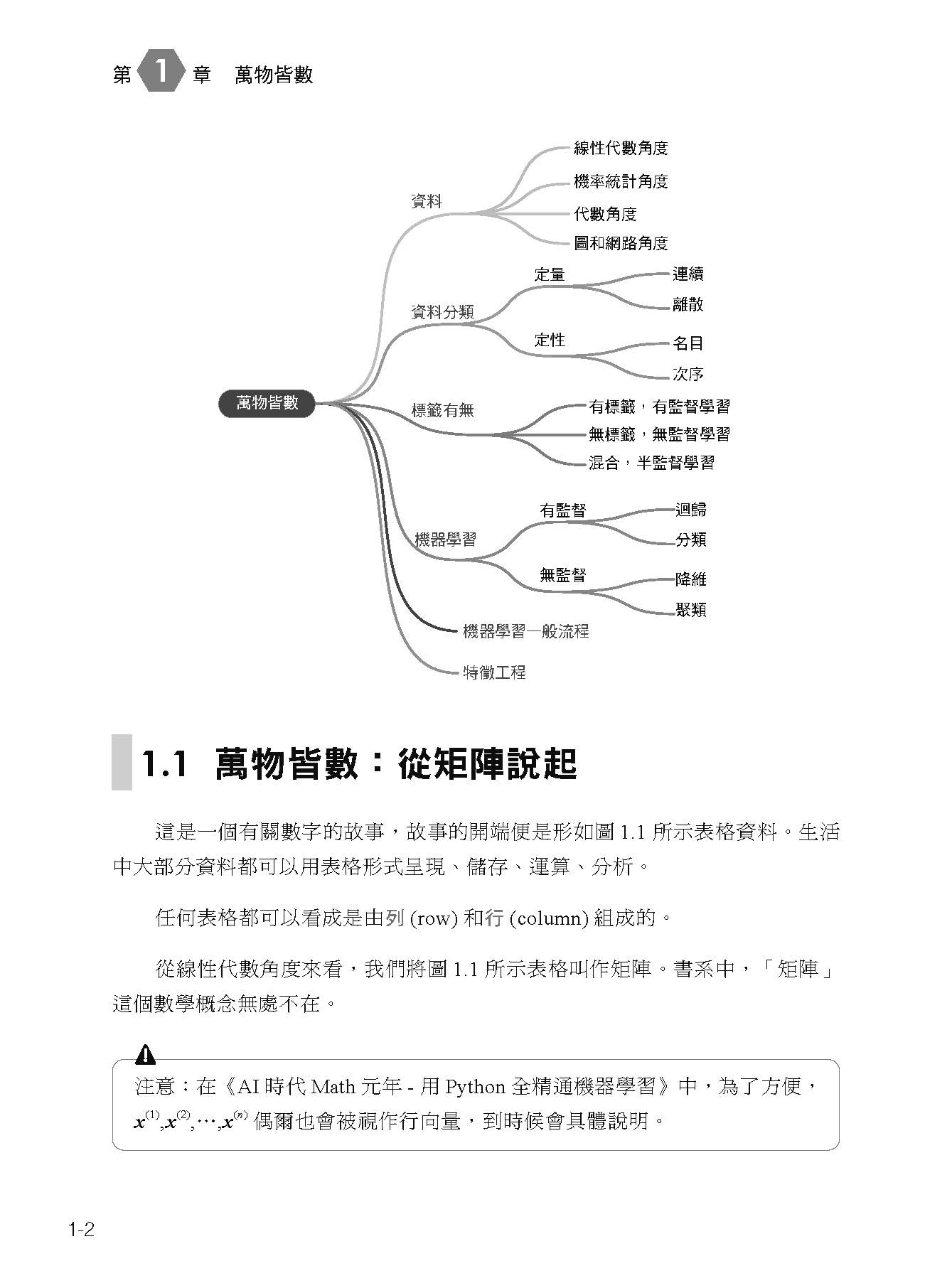
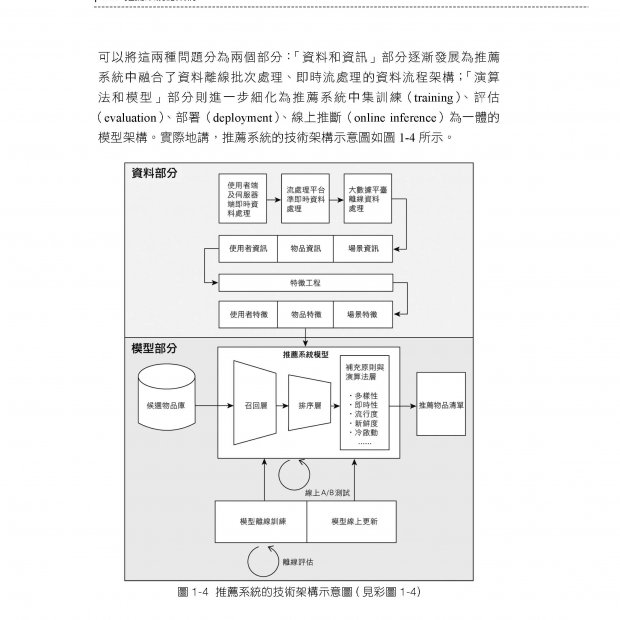
Chapter 1 萬物皆數 1.1 萬物皆數:從矩陣說起 1.2 資料分類:定量 ( 連續、離散 )、定性 ( 名目、次序 ) 1.3 機器學習:四大類演算法 1.4 特徵工程:提取、轉換、建構資料
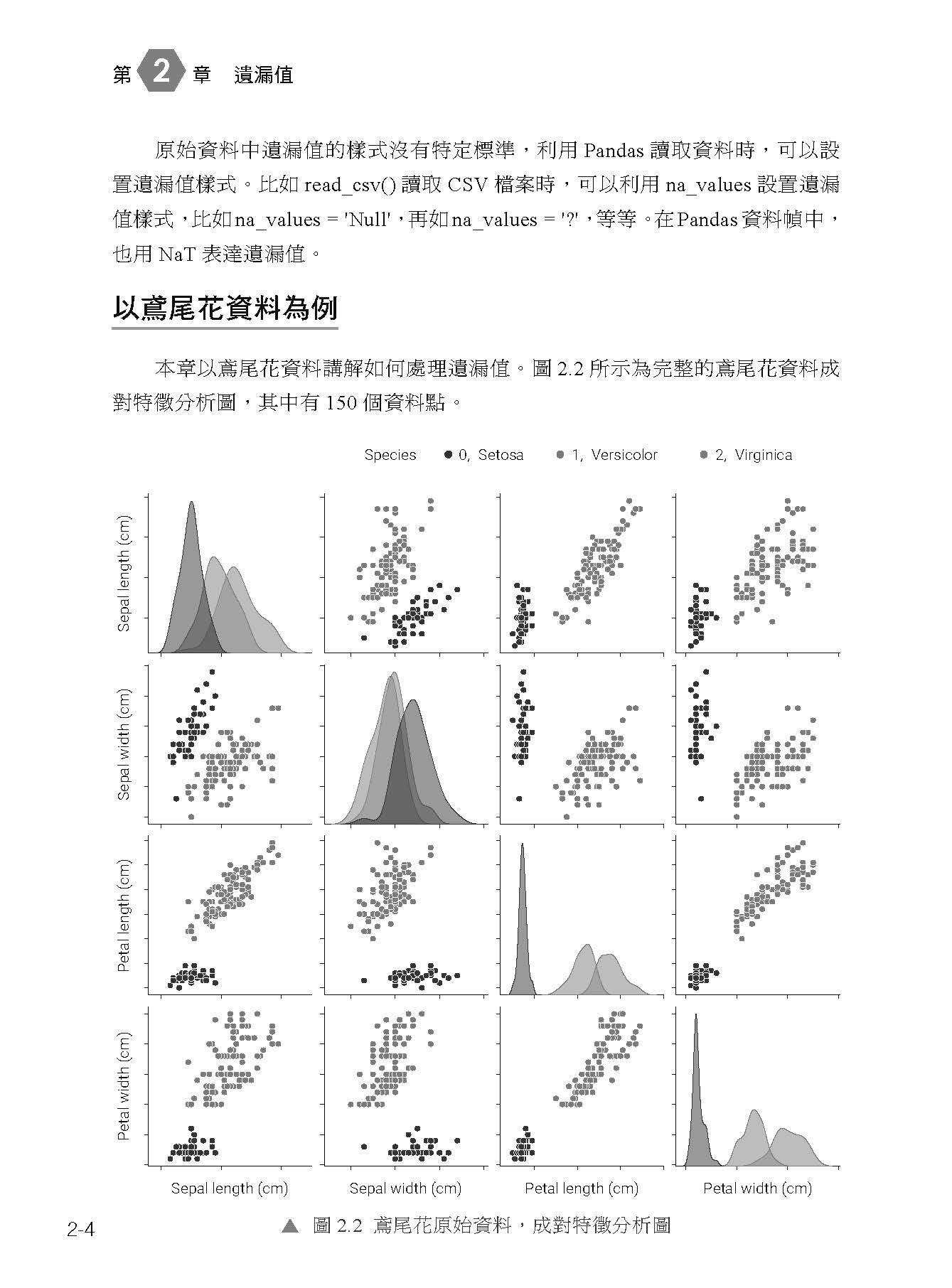
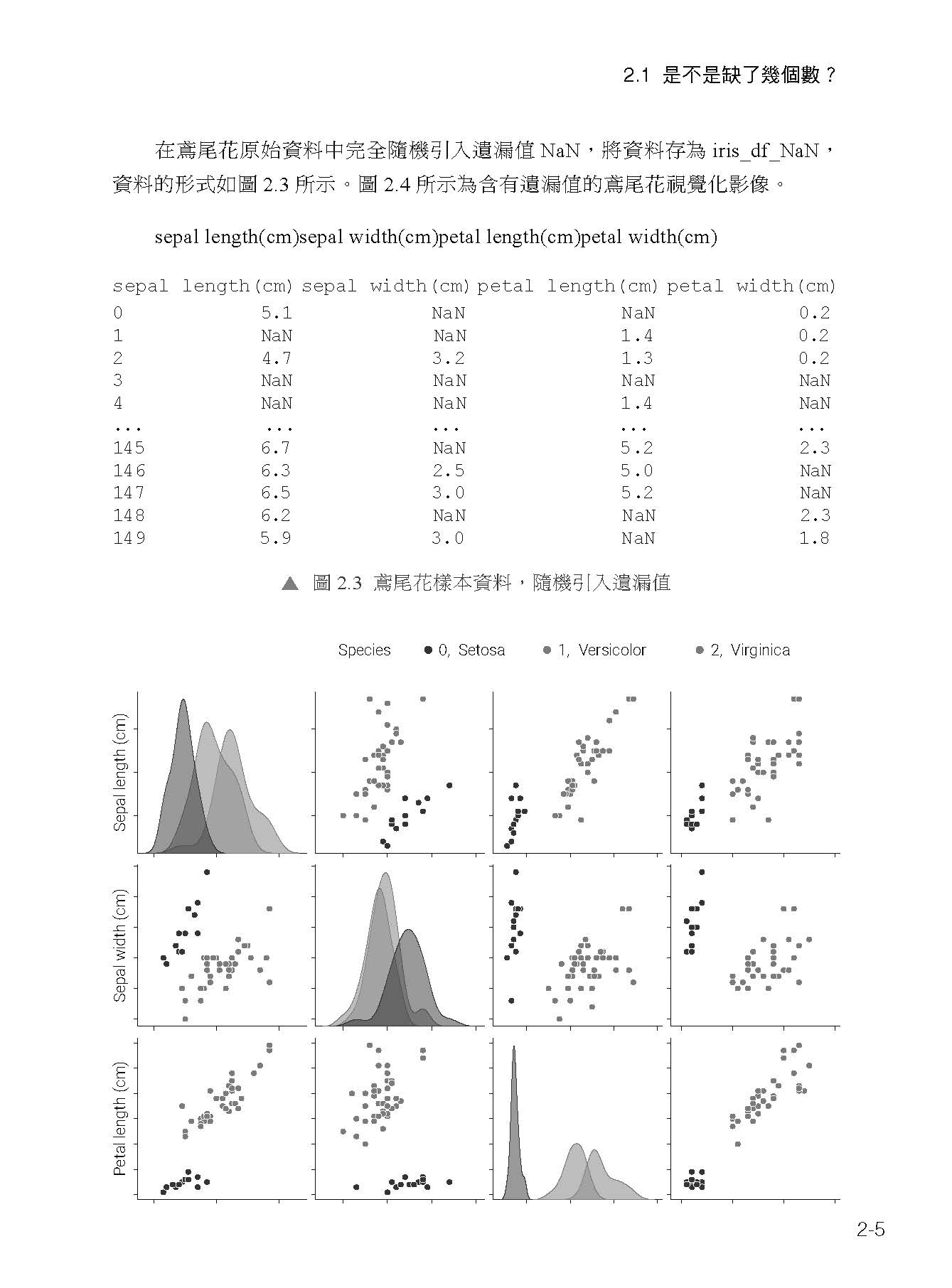
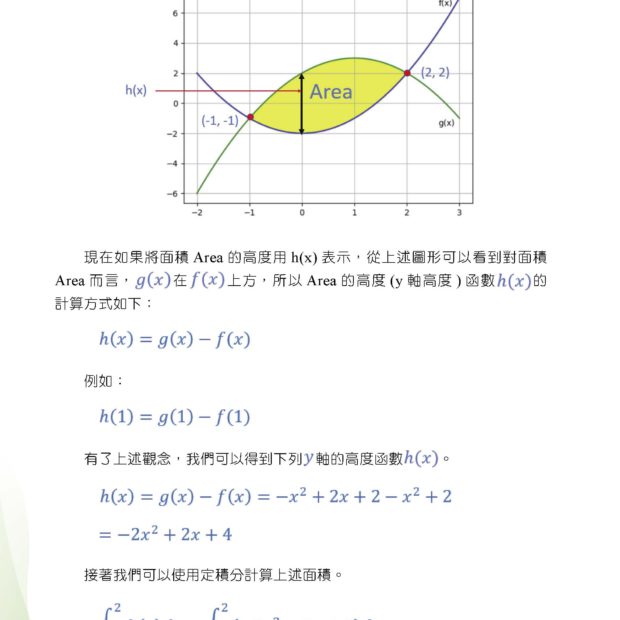
第2 篇 資料處理 Chapter 2 遺漏值 2.1 是不是缺了幾個數? 2.2 視覺化遺漏值位置 2.3 處理遺漏值:刪除 2.4 單變數插補 2.5 k 近鄰插補 2.6 多變數插補 Chapter 3 離群值 3.1 這幾個數有點不合群? 3.2 直方圖:單一特徵分布 3.3 散布圖:成對特徵分布 3.4 QQ 圖:分位數 - 分位數 3.5 箱型圖:上界、下界之外樣本 3.6 Z 分數:樣本資料標準化 3.7 馬氏距離和其他方法 Chapter 4 資料轉換 4.1 資料轉換 4.2 中心化:去平均值 4.3 標準化:Z 分數 4.4 歸一化:設定值在 0 和 1 之間 4.5 廣義冪轉換 4.6 經驗累積分布函式 4.7 插值 Chapter 5 資料距離 5.1 怎麼又聊距離? 5.2 歐氏距離:最常見的距離
5.3 標準化歐氏距離:考慮標準差 5.4 馬氏距離:考慮標準差和相關性 5.5 城市街區距離:L1 範數 5.6 謝比雪夫距離:L ∞範數 5.7 閔氏距離:Lp 範數 5.8 距離與親近度 5.9 成對距離、成對親近度 5.10 共變異數矩陣,為什麼無處不在?
第3篇 時間資料
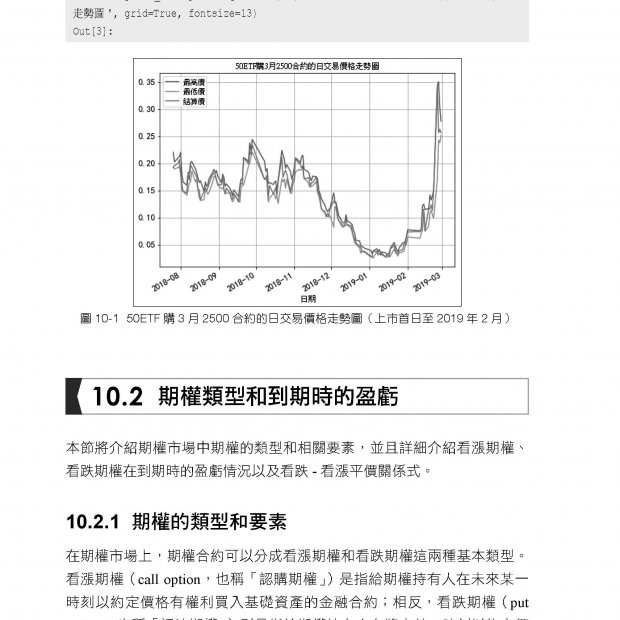
Chapter 6 時間資料 6.1 時間序列資料 6.2 處理時間序列遺漏值 6.3 從時間資料中發現趨勢 6.4 時間序列分解 6.5 時間資料講故事 Chapter 7 滾動視窗 7-1 滾動視窗 7.2 移動波動率 7.3 相關性 7.4 迴歸係數 7.5 指數加權移動平均 7.6 EWMA 波動率 Chapter 8 隨機過程入門 8.1 布朗運動:來自花粉顆粒無規則運動 8.2 無漂移布朗運動 8.3 漂移布朗運動:確定 + 隨機 8.4 具有一定相關性的布朗運動 8.5 幾何布朗運動 8.6 股價模擬 8.7 相關股價模擬 Chapter 9 高斯過程 9.1 高斯過程原理 9.2 共變異數矩陣 9.3 分塊共變異數矩陣 9.4 後驗 9.5 雜訊 9.6 核函式
第4篇 圖論基礎
Chapter 10 圖論入門 10.1 什麼是圖? 10.2 圖和幾何 10.3 圖和矩陣 10.4 圖和機器學習 10.5 NetworkX Chapter 11 無向圖 11.1 無向圖:邊沒有向 11.2 自環:節點到自身的邊 11.3 同構:具有等價關係的圖 11.4 多圖:同一對節點存在不止一條邊 11.5 子圖:圖的一部分 11.6 有權圖:邊附帶權重 Chapter 12 有向圖 12.1 有向圖:邊有向 12.2 外分支度、內分支度 12.3 鄰居:上家、下家 12.4 有向多圖:平行邊 12.5 三元組:三個節點的 16 種關係 12.6 NetworkX 建立圖 Chapter 13 圖的視覺化 13.1 節點位置 13.2 節點裝飾 13.3 邊裝飾 13.4 分別繪製節點和邊 第5篇 圖的分析 Chapter 14 常見圖 14.1 常見圖類型 14.2 完全圖 14.3 二分圖 14.4 正規圖 14.5 樹 14.6 柏拉圖圖 Chapter 15 從路徑說起 15.1 通道、軌跡、路徑、迴路、環 15.2 常見路徑問題 15.3 最短路徑問題 15.4 尤拉路徑 15.5 漢米爾頓路徑 15.6 推銷員問題 Chapter 16 連通性 16.1 連通性 16.2 連通分量 16.3 強連通、弱連通:有向圖 16.4 橋 Chapter 17 圖的分析 17.1 度分析 17.2 距離度量 17.3 中心性 17.4 圖的社區 第6 篇 圖與矩陣 Chapter 18 從圖到矩陣 18.1 無向圖到鄰接矩陣 18.2 有向圖到鄰接矩陣 18.3 傳球問題 18.4 鄰接矩陣的矩陣乘法 18.5 特徵向量中心性 Chapter 19 成對度量矩陣 19.1 成對距離矩陣 19.2 親近度矩陣:高斯核函式 19.3 相關性係數矩陣 Chapter 20 轉移矩陣 20.1 再看鄰接矩陣 20.2 轉移矩陣:可能性 20.3 有向圖 20.4 馬可夫鏈 Chapter 21 其他矩陣 21.1 圖中常見矩陣 21.2 連結矩陣 21.3 度矩陣 21.4 拉普拉斯矩陣
第7篇 圖論實踐
Chapter 22 樹 22.1 樹 22.2 最近共同祖先 22.3 最小生成樹 22.4 決策樹:分類演算法 22.5 層次聚類 22.6 樹狀圖:聚類演算法 Chapter 23 資料聚類 23.1 資料聚類 23.2 距離矩陣 23.3 相似度 23.4 無向圖 23.5 拉普拉斯矩陣 23.6 特徵值分解 Chapter 24 PageRank 演算法 24.1 PageRank 演算法 24.2 線性方程組 24.3 冪迭代 Chapter 25 社群網路分析 25.1 社群網路分析 25.2 度分析 25.3 圖距離 25.4 中心性 25.5 社區結構
|
序
| 感謝
首先感謝大家的信任。 作者僅是在學習應用資料科學和機器學習演算法時,多讀了幾本數學書,多做了一些思考和知識 整理而已。知者不言,言者不知。知者不博,博者不知。由於作者水準有限,斗膽把自己所學所思與大家分享,作者權當無知者無畏。希望大家在Github 多提意見,讓這套書成為作者和 讀者共同參與創作的作品。 特別感謝清華大學出版社的欒大成老師。從選題策劃、內容創作到裝幀設計,欒老師事無巨細、一路陪伴。每次與欒老師交流,都能感受到他對優質作品的追求、對知識分享的熱情。 出來混總是要還的 曾幾何時,考試是我們學習數學的唯一動力。考試是頭懸樑的繩,是錐刺股的錐。我們中的大多數人從小到大為各種考試埋頭題海,數學味同嚼蠟,甚至讓人恨之入骨。 數學所帶來了無盡的「折磨」。我們甚至恐懼數學,憎恨數學,恨不得一走出校門就把數學拋之腦後,老死不相往來。 可悲可笑的是,我們很多人可能會在畢業的五年或十年以後,因為工作需要,不得不重新學習微積分、線性代數、機率統計,悔恨當初沒有學好數學,甚至遷怒於教材和老師。 這一切不能都怪數學,值得反思的是我們學習數學的方法和目的。 再給自己一個學數學的理由 為考試而學數學,是被逼無奈的舉動。而為數學而數學,則又太過高尚而遙不可及。 相信對絕大部分的我們來說,數學是工具、是謀生手段,而非目的。我們主動學數學,是想用數學工具解決具體問題。 現在,這套書給大家一個「學數學、用數學」的全新動力– 資料科學、機器學習。 資料科學和機器學習已經深度融合到我們生活的各方面,而數學正是開啟未來大門的鑰匙。不是所有人生來都握有一副好牌,但是掌握「數學 + 程式設計 + 機器學習」的知識絕對是王牌。這次,學習數學不再是為了考試、分數、升學,而是投資時間、自我實現、面向未來。 未來已來,你來不來? |